Cómo identificar las cuatro secciones cónicas en forma de gráfico
Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el gráfico. Usted puede alterar la forma de cada uno de estos gráficos de varias maneras, pero las formas generales del gráfico sigue siendo fiel al tipo de curva que lo son.
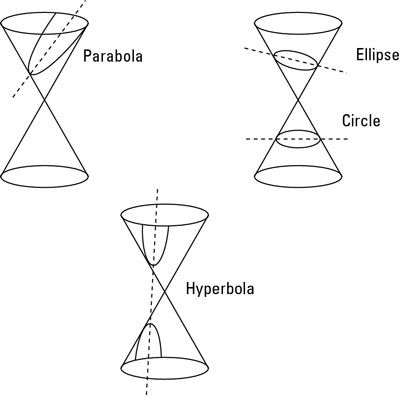
Esta figura ilustra cómo un avión cruza el cono (la mitad superior e inferior se consideran dos mitades de un cono) para crear las secciones cónicas, y la lista siguiente se explica la figura.
Círculo: Un círculo es el conjunto de todos los puntos que se encuentran a una distancia dada (el radio, r) A partir de un punto dado (el centro). Para conseguir un círculo desde el cono recto, las rodajas de plano horizontal se produce ya sea a través de la mitad superior o inferior del cono.
Parábola: Una parábola es una curva en la que cada punto es equidistante de un punto (el foco) y una línea (la directriz). Se parece mucho a la carta U, aunque puede ser al revés o de lado. Para formar una parábola, el plano corta a través paralelo al lado del cono de la derecha).
Elipse: Una elipse es el conjunto de todos los puntos donde la suma de las distancias desde dos puntos (los focos) es constante. Usted puede estar más familiarizado con otro término para la elipse, oval. Con el fin de obtener una elipse desde el cono de la derecha, el avión debe cortar a través del cono en un ángulo lo suficientemente poco profunda donde se está rebanando a través de sólo la mitad del cono. (Nota:. Si las rodajas de plano horizontal a través del cono, se crea un círculo Un círculo es considerado un tipo especial de elipse.)
Hipérbola: Una hipérbola es el conjunto de puntos en los que la diferencia de las distancias entre dos puntos es constante. La forma de la hipérbola es difícil de describir sin una imagen, pero se ve visualmente como dos parábolas (aunque son muy diferentes matemáticamente) reflejando unos a otros con un poco de espacio entre ellos. Para obtener una hipérbola, el avión debe cortar a través de la cono recto y un ángulo lo suficientemente empinada donde está rebanando a través de ambas mitades del cono.
La mayoría de las veces, dibujando una cónica no es suficiente. Cada sección cónica tiene su propio conjunto de información que por lo general tiene que dar para complementar el gráfico. Hay que indicar donde se encuentran los de centro, vértices, ejes mayor y menor, y focos. A menudo, esta información es más importante que el propio gráfico. Además, sabiendo todo esto valiosa información le ayuda a trazar la gráfica con más precisión de lo que podía sin ella.
-
Cómo configurar su campo de visión en Google SketchUp 8 -
Matemáticas normas fundamentales comunes: propiedades geométricas como ecuaciones -
Completando el cuadrado para las secciones cónicas -
Las secciones cónicas en pre-cálculo - Encontrar las piezas clave de todas las hipérbolas
-
¿Cómo encontrar la ecuación de asíntotas
Cómo graficar un círculo La primera cosa que hay que saber para graficar la ecuación de un círculo es donde en un plano se encuentra el centro. La ecuación de un círculo aparece comoEsto se llama el centro-radio forma (o formulario estándar), ya que le da dos piezas de…
Cómo representar gráficamente una parábola horizontal Una parábola horizontal cuenta con sus propias ecuaciones para encontrar su partes- estos son sólo un poco diferente en comparación con una parábola vertical. La distancia al foco y la directriz desde el vértice en este caso es horizontal,…
Cómo graficar una hipérbola en 5 pasos Al graficar una hipérbola, se puede pensar que es una mezcla de dos parábolas - cada uno de ellos una imagen de espejo perfecto de la otra, y cada apertura de distancia el uno del otro. La definición matemática de una hipérbola es el conjunto…
Cómo graficar una hipérbola Piense de una hipérbola como una mezcla de dos parábolas - cada una de ellas una imagen de espejo perfecto de la otra, cada abertura de distancia el uno del otro. Los vértices de estos parábolas están a una distancia dada de separación, y se…
Cálculo: cómo representar gráficamente una elipse Una elipse es básicamente un círculo que ha sido aplastado, ya sea horizontal o verticalmente. Desde una perspectiva de pre-cálculo, un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada de tal manera que la…
Cómo representar gráficamente una parábola vertical, Con el fin de representar gráficamente una parábola correctamente, es importante tener en cuenta si es una horizontal o una parábola vertical. Esto es porque mientras que las variables y constantes en las ecuaciones para las dos curvas tienen el…
Cómo graficar una elipse Un elipse es un conjunto de puntos en un plano, la creación de un óvalo, forma curvada, de tal manera que la suma de las distancias desde cualquier punto de la curva a dos puntos fijos (la focos) Es una constante (siempre la misma). Una elipse es…
Cómo graficar las secciones cónicas en forma paramétrica A veces, su profesor de pre-cálculo puede pedirle que gráfico de una cónica en forma paramétrica. Forma paramétrica es una forma elegante de decir una forma en la que usted puede hacer frente a las cónicas que no se expresan fácilmente como…
2 maneras de graficar un círculo Círculos son fáciles de trabajar en pre-cálculo. Un círculo tiene un centro, un radio, y un montón de puntos, pero sigue pasos ligeramente diferentes, dependiendo de si está mostrando el gráfico de un círculo centrado en el origen o desde el…
Cómo graficar las secciones cónicas en forma polar basado en la excentricidad Al graficar las secciones cónicas en el plano polar, utiliza ecuaciones que dependen de un valor especial conocido como excentricidad, que describe la forma general de una sección cónica. El valor de la excentricidad de una cónica puede decirle…
Cómo identificar las cuatro secciones cónicas en forma de ecuación Cada sección cónica tiene su propia forma estándar de una ecuación con X- y y-variables que se pueden representar gráficamente en el plano de coordenadas. Usted puede escribir la ecuación de una sección cónica si se le da puntos clave en el…
Cómo trazar coordenadas polares Coordenadas polares son una adición muy útil a su caja de herramientas matemáticas, ya que permiten a resolver los problemas que serían muy feo si tuviera que depender de norma X- y y-coordenadas. Con el fin de comprender plenamente cómo trazar…