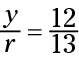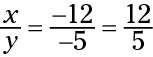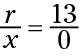Cómo calcular las coordenadas en el origen de cualquier círculo unidad
Usted no necesita un círculo unidad a utilizar esta coordenada negocio al determinar los valores de la función de los ángulos graficadas en posición estándar en un círculo. Puede utilizar un círculo con cualquier radio, siempre y cuando el centro está en el origen. La ecuación estándar para un círculo centrado en el origen es X2 + y2 = r2.
El uso de los ángulos que se muestran, encontrar el seno de alfa.
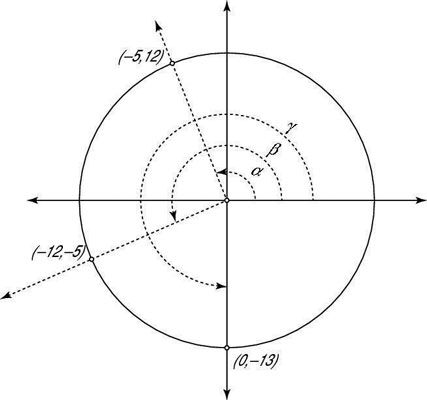
Encuentra el X- y y-coordenadas del punto en el lado terminal del ángulo de intersección con el círculo.
Las coordenadas son X = -5 Y y = 12.
Determinar el radio del círculo.
La ecuación del círculo es X2 + y2 = r2. Reemplazo de la X y y en esta ecuación con -5 y 12, respectivamente, se obtiene (-5)2 + (12)2 = 25 + 144 = 169 = r2. La raíz cuadrada de 169 es 13, por lo que el radio es 13.
Determinar la relación de la función y suplente en los valores.
La relación para el seno es y/r, lo que significa que sólo el necesario y-coordinar y radio, por lo que
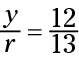
A continuación, utilizando los ángulos mostrados, encontrar la cotangente de la beta.
Encuentra el X- y y-coordenadas del punto en el lado terminal del ángulo de intersección con el círculo.
Las coordenadas son X = -12 Y y = -5.
La función cotangente utiliza sólo el X- y y-coordenadas, por lo que no es necesario resolver para el radio.
Determinar la relación de la función y suplente en los valores.
La relación de cotangente es X/y, así
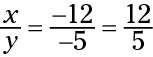
Ahora, con los ángulos mostrados, encontrar el secante de gamma.
Encuentra el X- y y-coordenadas del punto en el lado terminal del ángulo de intersección con el círculo.
Las coordenadas son X = 0 y y = -13.
Determinar el radio del círculo.
Por el primer ejemplo de esta sección, el radio es 13.
Determinar la relación de la función y suplente en los valores.
La relación de la secante es r/X, por lo que sólo la necesita X-coordinate- sustituyendo en, se obtiene
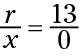
Esta respuesta es no definido, lo que significa que la gamma ángulo no secante.
Sobre el autor
 Cómo trazar los grandes ángulos de todo el círculo unidad
Cómo trazar los grandes ángulos de todo el círculo unidad Usted puede tomar los ángulos unidad de círculo y los triángulos rectángulos especiales y ponerlos juntos para crear un pequeño paquete: el círculo unidad completa. Usted crea triángulos especiales en el círculo unidad uno a la vez, porque…
 Cómo trazar coordenadas polares
Cómo trazar coordenadas polares Coordenadas polares son una adición muy útil a su caja de herramientas matemáticas, ya que permiten a resolver los problemas que serían muy feo si tuviera que depender de norma X- y y-coordenadas. Con el fin de comprender plenamente cómo trazar…
 Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica
Cómo utilizar identidades medio ángulo para evaluar una función trigonométrica Puede utilizar identidades-medio ángulo para evaluar una función trigonométrica de un ángulo que no está en el círculo unitario utilizando uno que sea. Por ejemplo, 15 grados, que no es en el círculo unitario, es la mitad de 30 grados, que se…
 Definir el radián en la trigonometría
Definir el radián en la trigonometría Introducción de una persona para ángulos es por lo general en términos de grados. Es probable que tenga una buena idea de lo que es un ángulo de 45 grados se parece. E incluso la mayoría de los estudiantes de secundaria saben que un triángulo…
 Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo
Cómo determinar la medida de un ángulo cuyo vértice se encuentra fuera de un círculo Un ángulo que cruza un círculo puede tener su vértice en el interior, sobre o fuera del círculo. Este artículo aborda los tres tipos de ángulos que tienen sus vértices fuera de un círculo: ángulos secante-secantes, ángulos…
 Ángulos en un círculo
Ángulos en un círculo Hay varias maneras de dibujo un ángulo en un círculo, y cada uno tiene una forma especial de calcular el tamaño de ese ángulo. Cuatro tipos diferentes de ángulos son: central, inscrito, interior, y exterior. Aquí, verá ejemplos de estos…
 Dominios y rangos de funciones trigonométricas
Dominios y rangos de funciones trigonométricas El dominio de una función se compone de todos los valores de entrada que una función puede manejar - la manera que la función está definida. Por supuesto, usted desea conseguir valores de salida (que conforman la gama) cuando introduce valores…
 Cómo calcular funciones trigonométricas usando cualquier círculo
Cómo calcular funciones trigonométricas usando cualquier círculo Cuando la determinación de los valores de la función trigonométrica de ángulos graficadas en la posición estándar en un círculo cuyo centro está en el origen, usted no tiene que tener un círculo unitario para calcular coordenadas. Puede…
 Cómo calcular las funciones trigonométricas de ángulos usando el círculo unitario
Cómo calcular las funciones trigonométricas de ángulos usando el círculo unitario Cálculo de funciones trigonométricas de ángulos dentro de un círculo unidad es muy fácil. La figura muestra un círculo unitario, que tiene la ecuación X2 + y2 = 1, junto con algunos puntos de la circunferencia y sus coordenadas.El uso de los…
 Cómo circunscribir un triángulo
Cómo circunscribir un triángulo Cada triángulo puede ser circunscrito por un círculo, lo que significa que un círculo - y sólo uno - pasa por los tres vértices (esquinas) de cualquier triángulo. En términos de los laicos, cualquier triángulo puede encajar en algún…
 ¿Cómo encontrar desaparecidos una coordenada en un círculo unitario
¿Cómo encontrar desaparecidos una coordenada en un círculo unitario Si usted tiene el valor de una de las coordenadas de un punto en el círculo unidad y necesita encontrar la otra, puede sustituir el valor conocido en la ecuación de la unidad de círculo y resolver para el valor perdido.Usted puede elegir…
 Cómo localizar ángulos de referencia
Cómo localizar ángulos de referencia Cada uno de los ángulos en un círculo unidad tiene un ángulo de referencia, que es siempre un ángulo agudo positivo (excepto los ángulos que ya son positivas y aguda). Al identificar el ángulo de referencia, se puede determinar los valores de…