Proving ángulos verticales son congruentes
Cuando dos líneas se cruzan para hacer una X, los ángulos en los lados opuestos de la X se denominan ángulos verticales. Estos ángulos son iguales, y aquí está el teorema oficial que lo dice.
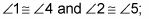
Los ángulos verticales son congruentes: Si dos ángulos son ángulos verticales, entonces son congruentes (ver la figura anterior).
Los ángulos verticales son una de las cosas más utilizados en las pruebas y otros tipos de problemas de geometría, y son una de las cosas más fáciles de detectar en un diagrama. No se olviden de comprobar por ellos!
Aquí hay un problema de geometría algebraica que ilustra este concepto simple: Determinar la medida de los seis ángulos en la siguiente figura.
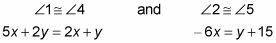
Los ángulos verticales son congruentes, así
y por lo tanto se puede establecer sus medidas iguales entre sí:
Ahora usted tiene un sistema de dos ecuaciones y dos incógnitas. Para resolver el sistema, primero resolver cada ecuación para y:
y = -3X
y = -6X - 15
A continuación, debido a que ambas ecuaciones se resuelven para y, puede configurar los dos X-expresiones iguales entre sí y resuelven por X:
-3X = -6X - 15
3X = -15
X = -5
Llegar y, conecte -5 para X en la primera ecuación simplificada:
y = -3X
y = -3 (-5)
y = 15
Ahora conecte -5 y 15 años en las expresiones ángulo para conseguir cuatro de los seis puntos de vista:
Para obtener el ángulo 3, nota que los ángulos 1, 2 y 3 hacen una línea recta, por lo que hay que sumar 180 # 176-:
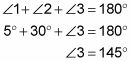
Por último, el ángulo 3 y el ángulo 6 son ángulos verticales congruentes, por lo que el ángulo 6 que haber 145 # 176- también. ¿Te diste cuenta que los ángulos de la figura son absurdamente fuera de escala? No olvide que usted no puede asumir nada acerca de los tamaños relativos de los ángulos o segmentos en un diagrama.
Cómo medir ángulos Ángulos de medición es bastante simple: el tamaño de un ángulo se basa en el ancho del ángulo está abierto. He aquí algunos puntos e imágenes mentales que le ayudarán a entender cómo funciona la medición de ángulos.Grado: La unidad…
¿Cómo demostrar ángulos son complementarios o suplementarios Ángulos complementarios son dos ángulos que suman 90 °, o un derecho de dos de ángulo cerrado ángulos suplementarios agregar hasta 180 °, o un ángulo recto. Estos ángulos no son las cosas más emocionantes en la geometría, pero usted tiene…
¿Cómo demostrar triángulos semejantes con sas ~ Usted puede probar que los triángulos son similares utilizando el método SAS ~ (Side-Angle-Side). SAS ~ establece que si dos lados de un triángulo son proporcionales a dos lados de otro triángulo y los ángulos incluidos son congruentes,…
¿Cómo demostrar triángulos semejantes usando el teorema de aa Usted puede utilizar el método de AA (ángulo-ángulo) para demostrar que los triángulos son semejantes. El teorema de AA establece que si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, entonces los triángulos…
Cómo utilizar CCTA después de probar triángulos semejantes CCTA es simplemente un acrónimo que significa "ángulos correspondientes de triángulos semejantes son congruentes. ' A menudo se utiliza CCTA en una prueba inmediatamente después de probar triángulos semejantes (exactamente de la misma manera…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
Propiedades de los paralelogramos Las propiedades del paralelogramo son simplemente aquellas cosas que son verdad en ello. Estas propiedades se refieren a sus lados, ángulos y diagonales.El paralelogramo tiene las siguientes propiedades:Los lados opuestos son paralelos, por…
Seis teoremas círculo importantes Los seis teoremas círculo discutidos aquí son sólo variaciones sobre una idea básica sobre la interconexión de los arcos, ángulos centrales y acordes (las seis se ilustran en la siguiente figura):Ángulos centrales y arcos:1.Si dos ángulos…
Trabajando con más de una transversal Cuando un dibujo de líneas paralelas-with-transversal contiene más de tres líneas, la identificación de ángulos congruentes y complementarias puede ser un poco difícil. La siguiente figura muestra dos líneas paralelas con dos transversales.Si…
Cifras trigonométricas básicas Segmentos, rayos y líneas son algunas de las formas básicas que se encuentran en la geometría, y son casi tan importantes en trigonometría. Utiliza esos segmentos, rayos y líneas para formar ángulos.Dibujo segmentos, rayos y líneasLA segmento…
Triángulos trigonométricas básicas Todo por su cuenta, los ángulos son sin duda muy emocionante. Pero los puso en un triángulo, y usted tiene la guinda del pastel. Triángulos son una de las figuras geométricas estudiadas con más frecuencia. Los ángulos que forman el triángulo…