Cómo utilizar CCTA después de probar triángulos semejantes
CCTA es simplemente un acrónimo que significa "ángulos correspondientes de triángulos semejantes son congruentes. ' A menudo se utiliza CCTA en una prueba inmediatamente después de probar triángulos semejantes (exactamente de la misma manera que se utilizan CPCTC después de probar congruentes los triángulos).
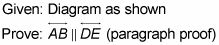
La siguiente prueba que muestra cómo funciona CCTA:
Así es como podría ir a su plan de juego: Cuando ves a los dos triángulos en este diagrama la prueba y se le pedirá que demostrar que las líneas son paralelas, usted debe estar pensando en la prueba de los triángulos similares. Luego, utilizando CCTA, tienes ángulos congruentes que se pueden utilizar con los teoremas de la línea paralela a terminar.
Así que aquí está la solución. Tienes el par de ángulos verticales congruentes, ángulo de 3 y 4 de ángulo, de modo que si usted podría demostrar que las partes que componen esos ángulos son proporcionales, los triángulos serían similares por SAS ~ (Side-Angle-Side). A fin de comprobar que los lados son proporcionales:
(Tenga en cuenta que la similitud está escrita de manera que los vértices correspondientes se emparejan.)
Cómo alinear polígonos similares Si se tienen problemas con un diagrama de polígonos similares que no se alinean en la misma orientación, considere volver a dibujar uno de ellos para que los dos están alineados en la misma forma. Esto puede hacer que el problema más fácil de…
Cómo hacer una prueba de paralelogramo Una buena manera de comenzar una prueba es pensar a través de un plan de juego que resume su argumento básico o de la cadena de la lógica. Los siguientes ejemplos de pruebas de paralelogramo muestran planes de juego seguidas por las pruebas…
¿Cómo demostrar que un cuadrilátero es un cometa Demostrando que un cuadrilátero es un cometa es un pedazo de pastel. Por lo general, todo lo que tienes que hacer es usar triángulos congruentes o triángulos isósceles. Estos son los dos métodos:Si dos pares disjuntos de lados consecutivos de…
¿Cómo demostrar triángulos semejantes con sas ~ Usted puede probar que los triángulos son similares utilizando el método SAS ~ (Side-Angle-Side). SAS ~ establece que si dos lados de un triángulo son proporcionales a dos lados de otro triángulo y los ángulos incluidos son congruentes,…
¿Cómo demostrar triángulos semejantes usando el teorema de aa Usted puede utilizar el método de AA (ángulo-ángulo) para demostrar que los triángulos son semejantes. El teorema de AA establece que si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, entonces los triángulos…
¿Cómo demostrar triángulos semejantes con sss ~ Usted puede probar que los triángulos son similares utilizando el método SSS ~ (Side-Side-Side). SSS ~ establece que si las relaciones de los tres pares de lados de dos triángulos correspondientes son iguales, entonces los triángulos son…
Cómo utilizar el teorema del ángulo bisectriz El teorema de ángulo-Bisectriz establece que si un rayo biseca un ángulo de un triángulo, a continuación, se divide el lado opuesto en segmentos que son proporcionales a los otros dos lados. La siguiente figura ilustra esto.El teorema de ángulo…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
Estrategias de prueba en la geometría Saber cómo escribir pruebas de geometría de dos columnas proporciona una base sólida para trabajar con teoremas. La práctica de estas estrategias le ayudará a escribir las pruebas de geometría fácilmente en poco tiempo:Hacer un plan de juego.…
Estrategias Prueba resumen Las siguientes estrategias pueden ayudarle mucho cuando estás trabajando en pruebas de geometría de dos columnas. Usted debe revisar estas estrategias y practicar el uso de ellos hasta que se convierten internalizada. Estas estrategias le hará…
Seis teoremas círculo importantes Los seis teoremas círculo discutidos aquí son sólo variaciones sobre una idea básica sobre la interconexión de los arcos, ángulos centrales y acordes (las seis se ilustran en la siguiente figura):Ángulos centrales y arcos:1.Si dos ángulos…