La aplicación de los teoremas transversales
Cuando se cruzan dos líneas con una tercera línea, la tercera línea se llama transversal. Puede utilizar los teoremas transversales para demostrar que los ángulos son congruentes o complementaria.
Aquí hay un problema que le permite echar un vistazo a algunos de los teoremas en acción: Teniendo en cuenta que las líneas m y n son paralelas, encontrar la medida del ángulo 1.
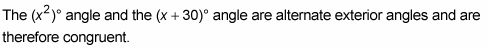
Aquí está la solución:
(O también se puede decir que porque tienes las líneas paralelas-plus-transversal diagrama y dos ángulos que son, obviamente, aguda, deben ser congruentes.) Establecer iguales entre sí y resolver X:
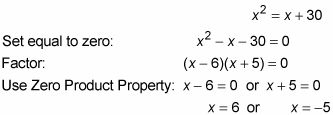
Esta ecuación tiene dos soluciones, a fin de tomar uno a la vez y conectarlos a las x en los ángulos alternos externos.
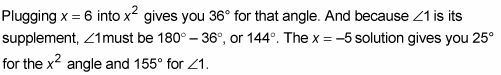
Así 144 # 176- y 155 # 176- son sus posibles respuestas para ángulo 1.
Cuando se obtienen dos soluciones (como X = 6 y X = -5) En un problema como este, no conecte uno de ellos en uno de los X's
y la otra solución en el otro X (como -5 + 30 = 25). Usted tiene que conectar una de las soluciones en todas X's, que le da un resultado para ambos ángulos
entonces usted tiene que conectar por separado la otra solución en todo X's, que le da un segundo resultado para ambos ángulos
Los ángulos y segmentos no pueden tener medidas o longitudes negativas. Asegúrese de que cada solución para X produce positivo respuestas para todas los ángulos o segmentos en un problema.
Si una solución hace que cualquier ángulo o segmento en el diagrama negativo, debe ser rechazada, incluso si los ángulos o segmentos que se preocupan por llegar a ser positivo. Sin embargo, no rechazar una solución justa causa X es negativo: X puede ser negativo, siempre y cuando los ángulos y segmentos son positivos (X = -5, Por ejemplo, funciona bien en este problema).
Ahora aquí está una prueba que utiliza algunos de los teoremas transversales:
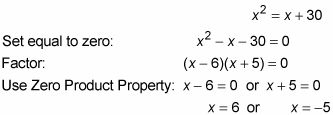
Echa un vistazo a la prueba formal:
Declaración 1:
Motivo de la declaración 1: Dada.
Declaración 2:
Motivo de la declaración 2: Dada.
Declaración 3:
Motivo de la declaración 3: Si las líneas son paralelas, entonces los ángulos alternos son congruentes.
Declaración 4:
Motivo de la declaración de 4: Dada.
Declaración 5:
Motivo de la declaración de 5: Si un segmento (segmento GJ) se resta de dos segmentos congruentes, entonces las diferencias son congruentes.
Declaración 6:
Motivo de la declaración 6: SAS (utilizando líneas 1, 3, y 5).
Declaración 7:
Motivo de la declaración 7: CPCTC (las partes correspondientes de congruentes los triángulos son congruentes).
Declaración 8:
Motivo de la declaración de 8: Si los ángulos alternos externos son congruentes, entonces las líneas son paralelas.
Extienda las líneas en problemas transversales. La ampliación de las líneas paralelas y transversales puede ayudar a ver cómo se relacionan los ángulos.
Por ejemplo, si usted tiene dificultades para ver ese ángulo K y el ángulo H son ángulos interiores de hecho alternativos (para el paso 3 de la prueba),
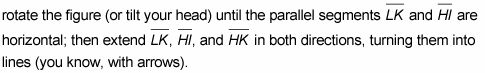
Después de hacer eso, usted está buscando en el esquema de línea paralela familiarizado se muestra en la siguiente figura.
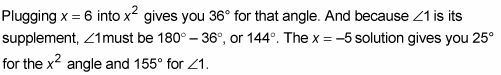
Usted puede hacer lo mismo para el ángulo LJK y el ángulo IGH mediante la ampliación
¿Cómo demostrar triángulos semejantes con sas ~ Usted puede probar que los triángulos son similares utilizando el método SAS ~ (Side-Angle-Side). SAS ~ establece que si dos lados de un triángulo son proporcionales a dos lados de otro triángulo y los ángulos incluidos son congruentes,…
¿Cómo demostrar triángulos semejantes usando el teorema de aa Usted puede utilizar el método de AA (ángulo-ángulo) para demostrar que los triángulos son semejantes. El teorema de AA establece que si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, entonces los triángulos…
¿Cómo demostrar que un cuadrilátero es un rectángulo Hay tres maneras de demostrar que un cuadrilátero es un rectángulo. Tenga en cuenta que los métodos segundo y tercero requieren que usted primera muestra (o recibirá) que el cuadrilátero en cuestión es un paralelogramo:Si todos los ángulos de…
¿Cómo demostrar triángulos semejantes con sss ~ Usted puede probar que los triángulos son similares utilizando el método SSS ~ (Side-Side-Side). SSS ~ establece que si las relaciones de los tres pares de lados de dos triángulos correspondientes son iguales, entonces los triángulos son…
¿Cómo demostrar que un cuadrilátero es un rombo Puede utilizar las seis siguientes métodos para demostrar que un cuadrilátero es un rombo. Los tres últimos métodos en esta lista requieren que usted primera muestra (o recibirá) que el cuadrilátero en cuestión es un paralelogramo:Si todos…
Cómo utilizar CCTA después de probar triángulos semejantes CCTA es simplemente un acrónimo que significa "ángulos correspondientes de triángulos semejantes son congruentes. ' A menudo se utiliza CCTA en una prueba inmediatamente después de probar triángulos semejantes (exactamente de la misma manera…
Estrategias de prueba en la geometría Saber cómo escribir pruebas de geometría de dos columnas proporciona una base sólida para trabajar con teoremas. La práctica de estas estrategias le ayudará a escribir las pruebas de geometría fácilmente en poco tiempo:Hacer un plan de juego.…
Estrategias Prueba resumen Las siguientes estrategias pueden ayudarle mucho cuando estás trabajando en pruebas de geometría de dos columnas. Usted debe revisar estas estrategias y practicar el uso de ellos hasta que se convierten internalizada. Estas estrategias le hará…
Proving ángulos verticales son congruentes Cuando dos líneas se cruzan para hacer una X, los ángulos en los lados opuestos de la X se denominan ángulos verticales. Estos ángulos son iguales, y aquí está el teorema oficial que lo dice.Los ángulos verticales son congruentes: Si dos…
Seis teoremas círculo importantes Los seis teoremas círculo discutidos aquí son sólo variaciones sobre una idea básica sobre la interconexión de los arcos, ángulos centrales y acordes (las seis se ilustran en la siguiente figura):Ángulos centrales y arcos:1.Si dos ángulos…
Los componentes de una prueba Una prueba de la geometría de dos columnas es un problema que involucra un diagrama geométrico de algún tipo. Le dicen una o más cosas que son verdaderas sobre el diagrama (el Givens), Y se le pide que probar que algo es verdad sobre el diagrama…
Trabajar con definiciones, teoremas y postulados Definiciones, teoremas y postulados son los componentes básicos de las pruebas de geometría. Con muy pocas excepciones, todas las justificaciones en la columna de la razón es una de estas tres cosas. La siguiente figura muestra un ejemplo de una…