Trabajar con definiciones, teoremas y postulados

Definiciones, teoremas y postulados son los componentes básicos de las pruebas de geometría. Con muy pocas excepciones, todas las justificaciones en la columna de la razón es una de estas tres cosas. La siguiente figura muestra un ejemplo de una prueba.

Si esto hubiera sido una prueba de geometría en lugar de un perro a prueba, la columna de la razón contendría si-entonces definiciones, teoremas y postulados acerca de la geometría en lugar de si-entonces ideas acerca de los perros. Aquí está la verdad sobre las definiciones, teoremas y postulados.

El uso de las definiciones en la columna de la razón

Definición: Una definición define o explica lo que significa un término. He aquí un ejemplo: " A punto medio divide un segmento en dos partes congruentes ".

Usted puede escribir todas las definiciones en si-entonces formar en cualquier dirección: " Si un punto es un punto medio de un segmento, entonces se divide ese segmento en dos partes congruentes " o " Si un punto divide a un segmento en dos partes congruentes, entonces es el punto medio de ese segmento ".

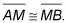
La figura de arriba muestra cómo utilizar las dos versiones de la definición del punto medio de una prueba de dos columnas.

Cuando usted tiene que elegir entre estas dos versiones de la definición del punto medio, recuerde que usted puede pensar en la palabra si en el sentido de porque yo ya sé y la palabra después en el sentido de Ahora puedo deducir. Por ejemplo, por razones 2 en la primera prueba en la figura, se elige la versión que se va, "Si un punto es el punto medio de un segmento, después se divide el segmento en dos partes congruentes, " porque ya sabes que M es el punto medio de

(porque se ha dado) ya partir de ese hecho dado se puede deducir que

El uso de teoremas y postulados en la columna de la razón

Teorema y postulado: Ambos teoremas y postulados son afirmaciones de la verdad geométrica, como Todos los ángulos rectos son congruentes o Todos los radios de un círculo son congruentes. La diferencia entre los postulados y teoremas es que los postulados son asumidos para ser verdad, pero teoremas debe ser probado para ser verdad basada en postulados y / o teoremas ya demostrados. Esta distinción no es algo que tienes que cuidar mucho de no ser que se esté escribiendo su Ph.D. disertación sobre la estructura deductiva de la geometría. Sin embargo, como es probable que estés no Actualmente trabaja en su doctorado en la geometría, no debería sudar este punto bien.

Escrito en si-entonces formar, el teorema Todas ángulos rectos son congruentes leería, " Si dos ángulos son rectos, entonces son congruentes ". A diferencia de las definiciones, teoremas son generalmente no reversible. Por ejemplo, si se invierte este derecho; teorema ángulo, se obtiene una declaración falsa: " Si dos ángulos son congruentes, entonces son ángulos rectos ". (Si un teorema funciona en ambas direcciones, obtendrá un teorema separado para cada versión Los dos teoremas isósceles-triángulo. - Si lados, entonces los ángulos y Si ángulos, luego lados - son un ejemplo) La figura anterior muestra la derecha;. Teorema del ángulo en una prueba.

Cuando usted está haciendo sus primeras pruebas, o más tarde si estás luchando con un año difícil, es muy útil para escribir sus razones (definiciones, teoremas y postulados) en si-entonces formulario. Cuando se utiliza si-entonces la forma, la estructura lógica de la prueba es más fácil de seguir. Después de convertirse en un experto en la prueba, se puede abreviar sus razones en la nosi-entonces formar o simplemente escriba el nombre de la definición, el teorema o postulado.