¿Cómo demostrar que un cuadrilátero es un rectángulo
Hay tres maneras de demostrar que un cuadrilátero es un rectángulo. Tenga en cuenta que los métodos segundo y tercero requieren que usted primera muestra (o recibirá) que el cuadrilátero en cuestión es un paralelogramo:
Si todos los ángulos de un cuadrilátero son ángulos rectos, entonces es un rectángulo (inversa de la definición rectángulo). (En realidad, sólo es necesario demostrar que los tres ángulos son rectos - si lo son, el cuarto es automáticamente un ángulo recto también.)
Si las diagonales de un paralelogramo son congruentes, entonces es un rectángulo (ni el reverso de la definición ni a la inversa de una propiedad).
Si un paralelogramo contiene un ángulo recto, entonces es un rectángulo (ni el reverso de la definición ni a la inversa de una propiedad).
Consejo: Haga lo siguiente para visualizar qué este método funciona: Tome una caja de cereales vacía y empuje en las solapas superiores. Si a continuación, mire en la caja vacía, la parte superior de la caja hace una forma rectangular, ¿verdad? Ahora, comienza a aplastar a la parte superior de la caja - ya sabes, como usted quiere que sea plana antes de meterla en la basura. Como empezar a aplastar a la parte superior del cuadro, se ve una forma de paralelogramo. Ahora, después de haber aplastado un poco, si usted toma este paralelogramo y hacer uno de los ángulos de un ángulo recto, toda la parte superior tiene que convertirse en un rectángulo de nuevo. No se puede hacer uno de los ángulos de un ángulo recto y sin los otros tres también se conviertan en ángulo recto.
Antes de examinar cualquiera de estos métodos de prueba en acción, aquí hay un pequeño teorema útil que usted tiene que hacer la próxima prueba.
Ángulos suplementarios congruentes son ángulos rectos: Si dos ángulos son a la vez complementarias y congruentes, entonces son ángulos rectos. Esta idea tiene sentido porque 90 # 176- + 90 # 176- = 180 # 176-.
Muy bien, así que aquí está la prueba:
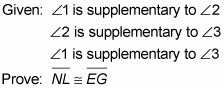
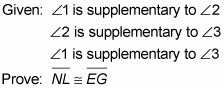
Declaración 1:
Motivo de la declaración 1: Dada.
Declaración 2:
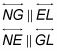
Motivo de la declaración 2: Si ángulos exteriores del mismo lado son suplementarios, entonces las líneas son paralelas.
Declaración 3:
Motivo de la declaración 3: Si ambos pares de lados opuestos de un cuadrilátero son paralelos, entonces el cuadrilátero es un paralelogramo.
Declaración 4:
Motivo de la declaración de 4: Si dos ángulos son suplementarios al mismo ángulo, entonces son congruentes.
Declaración 5:
Motivo de la declaración de 5: Dada.
Declaración 6:
Motivo de la declaración 6: Si dos ángulos son a la vez complementarias y congruentes, entonces son ángulos rectos.
Declaración 7:
Motivo de la declaración 7: Si las líneas forman un ángulo recto, entonces son perpendiculares.
Declaración 8:
Motivo de la declaración de 8: Si las líneas son perpendiculares, entonces forman ángulos rectos.
Declaración 9:
Motivo de la declaración 9: Si un paralelogramo contiene un ángulo recto, entonces es un rectángulo.
Declaración 10:
Motivo de la declaración de 10: Las diagonales de un rectángulo son congruentes.
¿Cómo demostrar que un cuadrilátero es un cuadrado Hay cuatro métodos que puede utilizar para demostrar que un cuadrilátero es un cuadrado. En los últimos tres de estos métodos, primero tiene que demostrar (o ser dado) que el cuadrilátero es un rectángulo, rombo, o ambos:Si un cuadrilátero…
¿Cómo demostrar ángulos son complementarios o suplementarios Ángulos complementarios son dos ángulos que suman 90 °, o un derecho de dos de ángulo cerrado ángulos suplementarios agregar hasta 180 °, o un ángulo recto. Estos ángulos no son las cosas más emocionantes en la geometría, pero usted tiene…
¿Cómo demostrar que un cuadrilátero es un cometa Demostrando que un cuadrilátero es un cometa es un pedazo de pastel. Por lo general, todo lo que tienes que hacer es usar triángulos congruentes o triángulos isósceles. Estos son los dos métodos:Si dos pares disjuntos de lados consecutivos de…
¿Cómo demostrar triángulos semejantes usando el teorema de aa Usted puede utilizar el método de AA (ángulo-ángulo) para demostrar que los triángulos son semejantes. El teorema de AA establece que si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, entonces los triángulos…
¿Cómo demostrar que un cuadrilátero es un rombo Puede utilizar las seis siguientes métodos para demostrar que un cuadrilátero es un rombo. Los tres últimos métodos en esta lista requieren que usted primera muestra (o recibirá) que el cuadrilátero en cuestión es un paralelogramo:Si todos…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
La identificación de los siete cuadriláteros Un cuadrilátero es un polígono de cuatro lados. Hay siete cuadriláteros, algunos que son sin duda familiar para usted, y algunos que puede no ser tan familiar. Echa un vistazo a las siguientes definiciones y el árbol genealógico de…
Propiedades de los paralelogramos Las propiedades del paralelogramo son simplemente aquellas cosas que son verdad en ello. Estas propiedades se refieren a sus lados, ángulos y diagonales.El paralelogramo tiene las siguientes propiedades:Los lados opuestos son paralelos, por…
Propiedades de rombos, rectángulos y cuadrados Los tres paralelogramos especiales - rombo, rectángulo y cuadrado - son los llamados porque son casos especiales del paralelogramo. (Además, la plaza es un caso especial o escribe tanto del rectángulo y rombo.)La jerarquía de tres niveles que se…
Proving ángulos verticales son congruentes Cuando dos líneas se cruzan para hacer una X, los ángulos en los lados opuestos de la X se denominan ángulos verticales. Estos ángulos son iguales, y aquí está el teorema oficial que lo dice.Los ángulos verticales son congruentes: Si dos…
Seis teoremas círculo importantes Los seis teoremas círculo discutidos aquí son sólo variaciones sobre una idea básica sobre la interconexión de los arcos, ángulos centrales y acordes (las seis se ilustran en la siguiente figura):Ángulos centrales y arcos:1.Si dos ángulos…
Trabajar con definiciones, teoremas y postulados Definiciones, teoremas y postulados son los componentes básicos de las pruebas de geometría. Con muy pocas excepciones, todas las justificaciones en la columna de la razón es una de estas tres cosas. La siguiente figura muestra un ejemplo de una…