Propiedades de rombos, rectángulos y cuadrados
Los tres paralelogramos especiales - rombo, rectángulo y cuadrado - son los llamados porque son casos especiales del paralelogramo. (Además, la plaza es un caso especial o escribe tanto del rectángulo y rombo.)
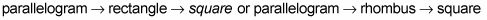
La jerarquía de tres niveles que se ve con
en el árbol genealógico de cuadrilátero anterior funciona igual que
Un perro es un tipo especial de un mamífero y un dálmata es un tipo especial de un perro.
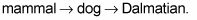
Estas son las propiedades del rombo, rectángulo y cuadrado. Tenga en cuenta que debido a que estos tres cuadriláteros son paralelogramos, sus propiedades incluyen las propiedades de paralelogramo.
El rombo tiene las siguientes propiedades:
Todas las propiedades de un paralelogramo se aplican (los que importan aquí son caras paralelas, los ángulos opuestos son congruentes y ángulos consecutivos son suplementarios).
Todos los lados son congruentes por definición.
Las diagonales bisecan los ángulos.
Las diagonales son las mediatrices de cada uno.
El rectángulo tiene las siguientes propiedades:
Todas las propiedades de un paralelogramo se aplican (los que importan aquí son lados paralelos, lados opuestos son congruentes y diagonales bisecan).
Todos los ángulos son rectos, por definición.
Las diagonales son congruentes.
La plaza tiene las siguientes propiedades:
Todas las propiedades de un rombo se aplican (los que importan aquí son lados paralelos, diagonales son mediatrices de los demás, y diagonales bisecan los ángulos).
Todas las propiedades de un rectángulo se aplican (la única que importa aquí es diagonales son congruentes).
Todos los lados son congruentes por definición.
Todos los ángulos son rectos, por definición.
Ahora trata de trabajar a través de un problema. Dado el rectángulo como se muestra, encontrará las medidas de ángulo de 1 y el ángulo 2:
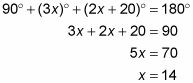
Aquí está la solución: MNPQ es un rectángulo, de modo ángulo Q = 90 °. Por lo tanto, debido a que hay 180 ° en un triángulo, se puede decir
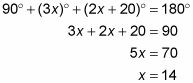
Ahora conecte 14 para toda la X'S.
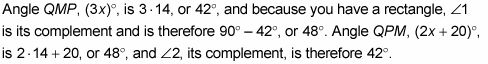
Ahora encontrar el perímetro de rombo RHOM.
Aquí está la solución: Todos los lados de un rombo son congruentes, así HO es igual a X + 2. Y debido a que las diagonales de un rombo son perpendiculares, triángulo HBO es un triángulo rectángulo. Terminas con el teorema de Pitágoras:
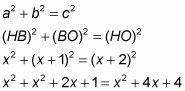
Combine los términos semejantes y establecer igual a cero:
Factor:
(X - 3) (X + 1) = 0
Use Zero Producto propiedad:
X - 3 = 0 o X + 1 = 0
X = 3 orx = -1
Usted puede rechazar X = -1 Debido a que se traduciría en triángulo HBO que tiene las piernas con longitudes de 1 y 0.
Fórmulas de geometría que usted debe saber A continuación se presentan algunas de las fórmulas de geometría más importantes, teoremas, propiedades, etc. que se utilizan para resolver diversos problemas. Si te quedas perplejo mientras se trabaja en un problema y no puede llegar a una…
Cómo calcular el área de un cuadrilátero Hay cinco fórmulas que se pueden utilizar para calcular el área de las siete cuadriláteros especiales. Sólo hay cinco fórmulas debido a que algunos de ellos lo hacen una doble función - por ejemplo, se puede calcular el área de un rombo con…
Cómo calcular el área de un paralelogramo, cometa, o trapezoidal Las fórmulas del área para el paralelogramo, cometa, y trapezoide se basan en el área de un rectángulo. Las siguientes figuras muestran cómo cada uno de estos tres cuadriláteros se refiere a un rectángulo, y la siguiente lista te da los…
¿Cómo demostrar que un cuadrilátero es un paralelogramo Hay cinco formas en que se puede demostrar que un cuadrilátero es un paralelogramo. Los cuatro primeros son los conversos de propiedades paralelogramo (incluida la definición de un paralelogramo). Asegúrese de recordar el curioso personaje quinto…
¿Cómo demostrar que un cuadrilátero es un cuadrado Hay cuatro métodos que puede utilizar para demostrar que un cuadrilátero es un cuadrado. En los últimos tres de estos métodos, primero tiene que demostrar (o ser dado) que el cuadrilátero es un rectángulo, rombo, o ambos:Si un cuadrilátero…
¿Cómo demostrar que un cuadrilátero es un cometa Demostrando que un cuadrilátero es un cometa es un pedazo de pastel. Por lo general, todo lo que tienes que hacer es usar triángulos congruentes o triángulos isósceles. Estos son los dos métodos:Si dos pares disjuntos de lados consecutivos de…
¿Cómo demostrar que un cuadrilátero es un rectángulo Hay tres maneras de demostrar que un cuadrilátero es un rectángulo. Tenga en cuenta que los métodos segundo y tercero requieren que usted primera muestra (o recibirá) que el cuadrilátero en cuestión es un paralelogramo:Si todos los ángulos de…
¿Cómo demostrar que un cuadrilátero es un rombo Puede utilizar las seis siguientes métodos para demostrar que un cuadrilátero es un rombo. Los tres últimos métodos en esta lista requieren que usted primera muestra (o recibirá) que el cuadrilátero en cuestión es un paralelogramo:Si todos…
Cómo diversos cuadriláteros están relacionados El árbol genealógico de cuadrilátero en la figura siguiente muestra las relaciones entre los diferentes cuadriláteros. La siguiente lista de preguntas que le da un sabor de algunas de estas relaciones. (Puede probarse a sí mismo mediante el…
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
La identificación de los siete cuadriláteros Un cuadrilátero es un polígono de cuatro lados. Hay siete cuadriláteros, algunos que son sin duda familiar para usted, y algunos que puede no ser tan familiar. Echa un vistazo a las siguientes definiciones y el árbol genealógico de…