Definiciones y teoremas de líneas paralelas
Las líneas paralelas son importantes cuando se estudia cuadriláteros porque seis de los siete tipos de cuadriláteros (todos ellos, excepto la cometa) contienen líneas paralelas. Los ocho ángulos formados por líneas paralelas y una transversal o son congruentes o complementaria.
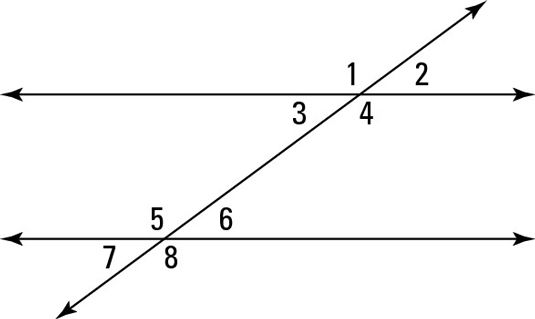
Echa un vistazo a la figura de arriba, que muestra tres líneas que se asemejan a un tipo de gigante no-signo igual. Las dos líneas horizontales son paralelas, y la tercera línea que los atraviesa se llama transversal. Como se puede ver, las tres líneas forman ocho ángulos.
Los siguientes teoremas le indican cómo diversos pares de ángulos se relacionan entre sí.
Demostrando que los ángulos son congruentes: Si una transversal interseca dos líneas paralelas, a continuación, los siguientes ángulos son congruentes (consulte la figura anterior):
Ángulos alternos: El par de ángulos 3 y 6 (así como 4 y 5) son ángulos alternos. Estos pares de ángulos están en (suplente) lados opuestos de la transversal y están en el medio (en el interior de) las líneas paralelas.
Ángulos alternos externos: Los ángulos 1 y 8 (y ángulos 2 y 7) son llamados ángulos alternos externos. Están en lados opuestos de la transversal, y están fuera de las líneas paralelas.
Ángulos correspondientes: El par de ángulos 1 y 5 (también 2 y 6, 3 y 7, y 4, y 8) están ángulos correspondientes. Los ángulos 1 y 5 se corresponden porque cada uno es en la misma posición (arriba a la izquierda, esquina) en su grupo de cuatro ángulos.
Observe también que los ángulos 1 y 4, 2 y 3, 5 y 8, y 6 y 7 son uno frente al otro, formando ángulos verticales, que también son congruentes.
Demostrando que los ángulos son suplementarios: Si una transversal interseca dos líneas paralelas, a continuación, los siguientes ángulos son suplementarios (véase la figura anterior):
Lo mismo del lado ángulos interiores: Ángulos 3 y 5 (y 4 y 6) están en el mismo lado de la transversal y están en el interior de las líneas paralelas, por lo que se llaman (listo para un choque?) ángulos interiores del mismo secundarios.
Lo mismo del lado ángulos exteriores: Los ángulos 1 y 7 (y 2 y 8) se denominan ángulos exteriores del mismo secundarios - que están en el mismo lado de la transversal, y están fuera de las líneas paralelas.
Puede resumir las definiciones y teoremas anteriores con la siguiente idea simple y concisa. Cuando se tienen dos líneas paralelas cortadas por una transversal, se obtiene cuatro ángulos agudos y cuatro ángulos obtusos (excepto cuando recibe ocho ángulos rectos). Todos los ángulos agudos son congruentes, todos los ángulos obtusos son congruentes, y cada ángulo agudo es complementaria a cada ángulo obtuso. En definitiva, cualquier dos de los ocho ángulos son o bien congruente o suplementario.
Demostrando que las líneas son paralelas: Todos estos teoremas funcionan a la inversa. Puede utilizar los siguientes teoremas para demostrar que las líneas son paralelas. Es decir, dos líneas son paralelas si están cortadas por una transversal tal que
Dos ángulos correspondientes son congruentes.
Dos ángulos alternos internos son congruentes.
Dos ángulos alternos externos son congruentes.
Dos ángulos interiores del mismo lado son suplementarios.
Dos ángulos exteriores del mismo lado son suplementarios.
¿Cómo demostrar ángulos son complementarios o suplementarios Ángulos complementarios son dos ángulos que suman 90 °, o un derecho de dos de ángulo cerrado ángulos suplementarios agregar hasta 180 °, o un ángulo recto. Estos ángulos no son las cosas más emocionantes en la geometría, pero usted tiene…
¿Cómo demostrar triángulos semejantes usando el teorema de aa Usted puede utilizar el método de AA (ángulo-ángulo) para demostrar que los triángulos son semejantes. El teorema de AA establece que si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, entonces los triángulos…
¿Cómo demostrar que un cuadrilátero es un rectángulo Hay tres maneras de demostrar que un cuadrilátero es un rectángulo. Tenga en cuenta que los métodos segundo y tercero requieren que usted primera muestra (o recibirá) que el cuadrilátero en cuestión es un paralelogramo:Si todos los ángulos de…
¿Cómo demostrar triángulos semejantes con sss ~ Usted puede probar que los triángulos son similares utilizando el método SSS ~ (Side-Side-Side). SSS ~ establece que si las relaciones de los tres pares de lados de dos triángulos correspondientes son iguales, entonces los triángulos son…
Cómo utilizar CCTA después de probar triángulos semejantes CCTA es simplemente un acrónimo que significa "ángulos correspondientes de triángulos semejantes son congruentes. ' A menudo se utiliza CCTA en una prueba inmediatamente después de probar triángulos semejantes (exactamente de la misma manera…
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
Propiedades de los paralelogramos Las propiedades del paralelogramo son simplemente aquellas cosas que son verdad en ello. Estas propiedades se refieren a sus lados, ángulos y diagonales.El paralelogramo tiene las siguientes propiedades:Los lados opuestos son paralelos, por…
Proving ángulos verticales son congruentes Cuando dos líneas se cruzan para hacer una X, los ángulos en los lados opuestos de la X se denominan ángulos verticales. Estos ángulos son iguales, y aquí está el teorema oficial que lo dice.Los ángulos verticales son congruentes: Si dos…
Seis teoremas círculo importantes Los seis teoremas círculo discutidos aquí son sólo variaciones sobre una idea básica sobre la interconexión de los arcos, ángulos centrales y acordes (las seis se ilustran en la siguiente figura):Ángulos centrales y arcos:1.Si dos ángulos…
Trabajando con más de una transversal Cuando un dibujo de líneas paralelas-with-transversal contiene más de tres líneas, la identificación de ángulos congruentes y complementarias puede ser un poco difícil. La siguiente figura muestra dos líneas paralelas con dos transversales.Si…
Cifras trigonométricas básicas Segmentos, rayos y líneas son algunas de las formas básicas que se encuentran en la geometría, y son casi tan importantes en trigonometría. Utiliza esos segmentos, rayos y líneas para formar ángulos.Dibujo segmentos, rayos y líneasLA segmento…
Triángulos trigonométricas básicas Todo por su cuenta, los ángulos son sin duda muy emocionante. Pero los puso en un triángulo, y usted tiene la guinda del pastel. Triángulos son una de las figuras geométricas estudiadas con más frecuencia. Los ángulos que forman el triángulo…