¿Cómo demostrar ángulos son complementarios o suplementarios

Ángulos complementarios son dos ángulos que suman 90 °, o un derecho de dos de ángulo cerrado ángulos suplementarios agregar hasta 180 °, o un ángulo recto. Estos ángulos no son las cosas más emocionantes en la geometría, pero usted tiene que ser capaz de detectar en un diagrama y saber utilizar los teoremas relacionados en pruebas.

Utiliza los teoremas mencionados aquí por ángulos complementarios:

• Complementos de el mismo ángulo son congruentes. Si dos ángulos son cada uno complementario a una tercera ángulo, a continuación, son congruentes entre sí. (Tenga en cuenta que este teorema implica tres ángulos totales.)

• Complementos de ángulos congruentes son congruentes. Si dos ángulos son complementarios a otros dos ángulos congruentes, entonces son congruentes. (Este teorema implica cuatro ángulos totales.)

Los siguientes ejemplos muestran lo increíblemente sencilla la lógica de estos dos teoremas es.

Complementos del mismo ángulo

Teniendo en cuenta: Diagrama como se muestra

Complementos de Ángulos congruentes

Teniendo en cuenta: Diagrama como se muestra

Nota: La lógica se muestra en estas dos figuras funciona de la misma cuando no se conoce el tamaño de los ángulos dados

Y aquí están los dos teoremas sobre ángulos complementarios que funcionan exactamente de la misma manera que los dos teoremas de ángulos complementarios:

• * Los suplementos de el mismo ángulo son congruentes. Si dos ángulos son cada uno complementario a un tercer ángulo, a continuación, son congruentes entre sí. (Esta es la versión de tres ángulos.)

• * Suplementos de ángulos congruentes son congruentes. Si dos ángulos son suplementarios a los otros dos ángulos congruentes, entonces son congruentes. (Esta es la versión de cuatro ángulos.)

Los cuatro teoremas anteriores acerca de ángulos complementarios y suplementarios vienen en pares: Uno de los teoremas implica de tres segmentos o ángulos, y el otro, que se basan en la misma idea, implica de cuatro segmentos o ángulos. Al hacer una prueba, tenga en cuenta si la parte correspondiente del diagrama de prueba contiene tres o cuatro segmentos o ángulos para determinar si se debe utilizar la versión de tres o cuatro objetos del teorema apropiado.

Echa un vistazo a uno de los teoremas complementaria de ángulo y uno de los teoremas complementario de ángulo en acción:

Antes de tratar de escribir una prueba formal, de dos columnas, a menudo es una buena idea pensar en un argumento asiento-de-los-pantalones acerca de por qué la probar declaración tiene que ser verdad. Piense en esto como un argumento plan de juego. Planes de juego son especialmente útiles para las pruebas más largas, ya que sin un plan, es posible que se perdió en medio de la prueba.

Cuando se trabaja a través de un plan de juego, puede que le resulte útil para compensar tamaños arbitrarios para segmentos y ángulos en la prueba. Usted puede hacer esto por segmentos y ángulos en los dados y, a veces, por segmentos y ángulos no mencionados. Usted no debe, sin embargo, compensar tamaños para las cosas que usted está tratando de mostrar son congruentes.

Plan de juego: En esta prueba, por ejemplo, usted podría decir a ti mismo: "Vamos a ver Debido a los segmentos perpendiculares dados, tiene dos ángulos rectos.....

Eso es.

Aquí está la prueba formal (cada declaración es seguida por la razón).

Declaración 1:

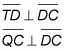
Motivo de la declaración 1: Dada. (¿Por qué te dicen esto? Ver razón 2.)

Declaración 2:

Motivo de la declaración 2: Si los segmentos son perpendiculares, entonces forman ángulos rectos (definición de la perpendicular).

Declaración 3:

Motivo de la declaración 3: Si dos ángulos forman un triángulo rectángulo, entonces son complementarios (definición de ángulos complementarios).

Declaración 4:

Motivo de la declaración de 4: Dada.

Declaración 5:

Motivo de la declaración 5: Si dos ángulos son complementarios a otros dos ángulos congruentes, entonces son congruentes.

Declaración 6:

Motivo de la declaración 6: Esto se supone a partir del diagrama.

Declaración 7:

Motivo de la declaración 7: Si dos ángulos forman un ángulo recto, entonces son suplementarios (definición de ángulos suplementarios).

Declaración 8:

Motivo de la declaración de 8: Si dos ángulos son suplementarios a los otros dos ángulos congruentes, entonces son congruentes.

Nota: Dependiendo de donde su profesor de geometría cae en la escala flojo-to-riguroso, él o ella podría permitir que usted omite un paso como el paso 6 en esta prueba porque es tan simple y obvio. Muchos maestros comienzan el primer semestre insistiendo en que se incluya cada pequeño paso, pero entonces, como el semestre avanza, se aflojan un poco y permiten saltarse algunos de los pasos más simples.