Cómo hacer una prueba de paralelogramo

Una buena manera de comenzar una prueba es pensar a través de un plan de juego que resume su argumento básico o de la cadena de la lógica. Los siguientes ejemplos de pruebas de paralelogramo muestran planes de juego seguidas por las pruebas formales resultantes.

Prueba 1

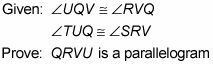
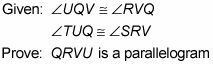
Aquí hay un plan de juego que expondrá cómo podría ir a su pensamiento:

• Observe los triángulos congruentes. Siempre verifique triángulos que parecen congruentes!

• Saltar a la final de la prueba y se pregunta si podría probar que QRVU es un paralelogramo si supieras que los triángulos son congruentes. Uso CPCTC (las partes correspondientes de congruentes los triángulos son congruentes), se podía demostrar que QRVU tiene dos pares de lados congruentes, y que haría un paralelogramo. Así. . .

• Averiguar cómo se puede demostrar que los triángulos son congruentes. Ya tiene segmento QV congruente consigo mismo por la propiedad reflexiva y un par de ángulos congruentes (da), y se puede obtener el otro ángulo de AAS (Angle-Angle-Side) con suplementos de ángulos congruentes. Eso lo hace.

Hay otras dos buenas maneras de hacer esto a prueba. Si te has dado cuenta que los ángulos congruentes dadas, UQV y RVQ, son ángulos alternos internos, que podría haber concluyó correctamente que los segmentos UQ y VR son paralelos. (Esta es una buena cosa para notar, así que felicitaciones si lo hizo.) Es posible que después de haber tenido la buena idea para tratar de demostrar que el otro par de lados paralelos por lo que podría utilizar el primer método de prueba de paralelogramo. Usted puede hacer esto mediante la prueba de los triángulos congruentes, utilizando CPCTC, y luego utilizando ángulos alternos VQR y QVU, pero asume, por el bien del argumento, que no te das cuenta de esto. Parecería como si estuvieras en un callejón sin salida. No dejes que esto te frustre. Al hacer las pruebas, no es raro que las buenas ideas y buenos planes para conducir a callejones sin salida. Cuando esto sucede, sólo tiene que ir de nuevo a la mesa de dibujo. Una tercera forma de hacer la prueba es conseguir ese primer par de líneas paralelas y luego demostrar que también son congruentes - con triángulos congruentes y CPCTC - y luego terminar con el método de prueba quinto paralelogramo.

Echa un vistazo a la prueba formal:

Declaración 1:

Motivo de la declaración 1: Dada.

Declaración 2:

Motivo de la declaración 2: Dada.

Declaración 3:

Motivo de la declaración 3: Si dos ángulos son suplementarios a los otros dos ángulos congruentes, entonces son congruentes.

Declaración 4:

Motivo de la declaración de 4: Propiedad reflexiva.

Declaración 5:

Motivo de la declaración de 5: AAS (3, 1, 4)

Declaración 6:

Motivo de la declaración 6: CPCTC (las partes correspondientes de congruentes los triángulos son congruentes).

Declaración 7:

Motivo de la declaración 7: CPCTC.

Declaración 8:

Motivo de la declaración de 8: Si ambos pares de lados opuestos de un cuadrilátero son congruentes, entonces el cuadrilátero es un paralelogramo.

Prueba 2

He aquí otra prueba - con un par de paralelogramos. Este problema te da más práctica con los métodos de prueba de paralelogramo, y porque es un poco más larga que la primera prueba, se le dará la oportunidad de pensar a través de un plan de juego más tiempo.

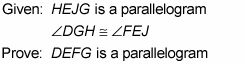
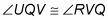
Su plan de juego podría ser algo como esto:

• Busque triángulos congruentes. Este diagrama se lleva la palma para contener triángulos congruentes - tiene seis pares de ellos! No pase mucho tiempo pensando en ellos - excepto los que pueden ayudarle - pero por lo menos hacer una nota mental rápida que están allí.

• Considere lo dado. Los ángulos congruentes dados, que son partes de

  

  son un gran indicio de que usted debe tratar de mostrar estos triángulos congruentes. Usted tiene los ángulos congruentes y los lados congruentes

  

  del paralelogramo HEJG, por lo que necesita sólo una más par de lados o ángulos congruentes utilizar SAS (Side-Angle-Side) o ASA (Ángulo-Lado-Ángulo).

• Piense en la final de la prueba.

  

  Así que usted debe tratar de la otra opción: la prueba de los triángulos congruentes con AAS.

  El segundo par de ángulos que había necesidad de ASA consiste en ángulo DHG y el ángulo FJE.

  

  Usted está en su camino.

• Considere métodos a prueba de paralelogramo. Ahora tiene un par de lados congruentes de DEFG. Dos de los métodos de prueba de paralelogramo utilizan un par de lados congruentes. Para completar uno de estos métodos, es necesario para mostrar uno de los siguientes:

• Que el otro par de lados opuestos son congruentes

• Ese segmento DG y el segmento de EF son paralelos, así como congruentes

Pregúntese qué enfoque se parece más fácil o más rápido.

¡Eso es un envoltorio!

Ahora echa un vistazo a la prueba formal:

Declaración 1:

Motivo de la declaración 1: Dada.

Declaración 2:

Motivo de la declaración 2: Los lados opuestos de un paralelogramo son congruentes.

Declaración 3:

Motivo de la declaración 3: Los lados opuestos de un paralelogramo son paralelas.

Declaración 4:

Motivo de la declaración de 4: Si las líneas son paralelas, ángulos exteriores continuación alternos son congruentes.

Declaración 5:

Motivo de la declaración de 5: Dada.

Declaración 6:

Motivo de la declaración 6: ASA (4, 2, 5).

Declaración 7:

Motivo de la declaración 7: CPCTC.

Declaración 8:

Motivo de la declaración de 8: CPCTC.

Declaración 9:

Motivo de la declaración 9: Si ángulos alternos internos son congruentes

a continuación, las líneas son paralelas.

Declaración 10:

Motivo de la declaración de 10: Si un par de lados opuestos de un cuadrilátero son a la vez paralelos y congruentes, entonces el cuadrilátero es un paralelogramo (líneas 9 y 7).