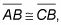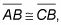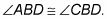Los componentes de una prueba
Una prueba de la geometría de dos columnas es un problema que involucra un diagrama geométrico de algún tipo. Le dicen una o más cosas que son verdaderas sobre el diagrama (el Givens), Y se le pide que probar que algo es verdad sobre el diagrama (el probar declaración). Cada prueba procede así:
Se empieza con uno o más de los hechos dados sobre el diagrama.
A continuación, declare algo que se deduce del hecho dado o hechos- entonces usted afirma algo que se desprende de eso- entonces, algo que se desprende de eso- y así sucesivamente. Cada deducción lleva a la siguiente.
Se termina haciendo su deducción final - el hecho de que usted está tratando de probar.
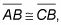
Cada, de dos columnas prueba de geometría estándar contiene los siguientes elementos. La maqueta de la prueba en la figura de arriba muestra cómo estos elementos encajan juntos.
El diagrama: La forma o formas en el diagrama son la materia objeto de la prueba. Su objetivo es demostrar algún hecho sobre el diagrama (por ejemplo, que dos triángulos o dos ángulos en el diagrama son congruentes). Los diagramas de prueba son generalmente, pero no siempre dibujan con precisión. No se olvide, sin embargo, que no se puede asumir que las cosas que se ven son verdad verdadera. Por ejemplo, sólo porque dos ángulos se ven congruentes, no significa que son.
Los dados: Los dados son verdaderos hechos sobre el diagrama que construir sobre para alcanzar su meta, la probar comunicado. Siempre comenzar una prueba con uno de los dados, poniéndolo en la línea 1 de la columna de la declaración.
La mayoría de la gente le gusta marcar el diagrama para mostrar la información de los dados. Por ejemplo, si uno de los Givens eran
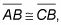
que le pone un poco de marca de la señal en ambos segmentos de modo que cuando usted echa un vistazo en el diagrama, la congruencia es inmediatamente evidente.
los probar declaración: los probar afirmación es el hecho sobre el diagrama que se debe establecer con su cadena de deducciones lógicas. Siempre va en la última línea de la columna de la declaración.
La columna declaración: En la columna de la declaración, que puso todos los hechos dados, los hechos que se deducen, y, en la última línea, las probar comunicado. En esta columna, se pone específico hechos acerca de específico objetos geométricos, tales como
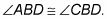
La columna razón: En la columna de la razón, se pone la justificación de cada declaración que usted hace. En esta columna, usted escribe reglas generales sobre las cosas en general, como Si es atravesada un ángulo, entonces se divide en dos partes congruentes. Usted no da los nombres de los objetos específicos.
Cómo medir segmentos de línea Para encontrar la medida o el tamaño de un segmento, sólo tiene que medir su longitud. ¿Qué más se puede medir? Después de todo, la longitud es la única característica tiene un segmento. Tienes tu resumen, su medio y sus segmentos largos.…
¿Cómo demostrar ángulos son complementarios o suplementarios Ángulos complementarios son dos ángulos que suman 90 °, o un derecho de dos de ángulo cerrado ángulos suplementarios agregar hasta 180 °, o un ángulo recto. Estos ángulos no son las cosas más emocionantes en la geometría, pero usted tiene…
¿Cómo demostrar que un cuadrilátero es un cometa Demostrando que un cuadrilátero es un cometa es un pedazo de pastel. Por lo general, todo lo que tienes que hacer es usar triángulos congruentes o triángulos isósceles. Estos son los dos métodos:Si dos pares disjuntos de lados consecutivos de…
¿Cómo demostrar triángulos semejantes usando el teorema de aa Usted puede utilizar el método de AA (ángulo-ángulo) para demostrar que los triángulos son semejantes. El teorema de AA establece que si dos ángulos de un triángulo son congruentes con dos ángulos de otro triángulo, entonces los triángulos…
¿Cómo demostrar que un cuadrilátero es un rectángulo Hay tres maneras de demostrar que un cuadrilátero es un rectángulo. Tenga en cuenta que los métodos segundo y tercero requieren que usted primera muestra (o recibirá) que el cuadrilátero en cuestión es un paralelogramo:Si todos los ángulos de…
¿Cómo demostrar que un cuadrilátero es un rombo Puede utilizar las seis siguientes métodos para demostrar que un cuadrilátero es un rombo. Los tres últimos métodos en esta lista requieren que usted primera muestra (o recibirá) que el cuadrilátero en cuestión es un paralelogramo:Si todos…
Cómo utilizar CCTA después de probar triángulos semejantes CCTA es simplemente un acrónimo que significa "ángulos correspondientes de triángulos semejantes son congruentes. ' A menudo se utiliza CCTA en una prueba inmediatamente después de probar triángulos semejantes (exactamente de la misma manera…
El dominio de la prueba formal de la geometría Supongamos que usted necesita para resolver un misterio crimen. Usted encuesta la escena del crimen, reunir los datos, y se anota en su bloc de notas. Para resolver el crimen, usted toma los hechos conocidos y, paso a paso, demuestra que cometió el…
Estrategias de prueba en la geometría Saber cómo escribir pruebas de geometría de dos columnas proporciona una base sólida para trabajar con teoremas. La práctica de estas estrategias le ayudará a escribir las pruebas de geometría fácilmente en poco tiempo:Hacer un plan de juego.…
Estrategias Prueba resumen Las siguientes estrategias pueden ayudarle mucho cuando estás trabajando en pruebas de geometría de dos columnas. Usted debe revisar estas estrategias y practicar el uso de ellos hasta que se convierten internalizada. Estas estrategias le hará…
Proving ángulos verticales son congruentes Cuando dos líneas se cruzan para hacer una X, los ángulos en los lados opuestos de la X se denominan ángulos verticales. Estos ángulos son iguales, y aquí está el teorema oficial que lo dice.Los ángulos verticales son congruentes: Si dos…
Trabajar con definiciones, teoremas y postulados Definiciones, teoremas y postulados son los componentes básicos de las pruebas de geometría. Con muy pocas excepciones, todas las justificaciones en la columna de la razón es una de estas tres cosas. La siguiente figura muestra un ejemplo de una…