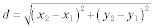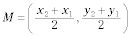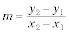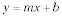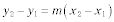LA polígono
es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo, triángulos rectángulos, las relaciones entre los ángulos y los lados de triángulos y ángulos interiores y exteriores de los polígonos.
Todos los triángulos
La suma de los tres ángulos interiores de un triángulo es 180 # 176-.
La mayor lado de un triángulo es opuesto al ángulo más grande del triángulo.
La suma de los dos lados más cortos de un triángulo debe ser mayor que el lado más largo del triángulo.
El ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores no adyacentes del triángulo.
los centroide de un triángulo divide cada mediana del triángulo en segmentos con una relación 2: 1.
Triángulos rectángulos
El teorema de Pitágoras que la2 + b2 = c2, dónde la y b representar los catetos del triángulo a la derecha y c representa la hipotenusa.
Al dibujar una altitud a la hipotenusa de un triángulo rectángulo, a formar dos triángulos rectángulos que son similares entre sí y también similar al triángulo original derecha. Debido a que estos triángulos son semejantes, puede configurar las siguientes proporciones:
La altitud a la hipotenusa de un triángulo rectángulo es la media proporcional entre los dos segmentos que la hipotenusa se divide en:
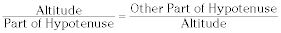
La pierna de un triángulo rectángulo es la media proporcional entre la hipotenusa y la proyección de la pierna de la hipotenusa:
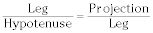
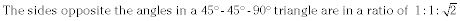
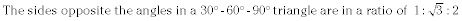
Aquí están las razones trigonométricas en un triángulo rectángulo:
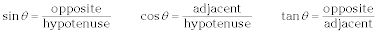
Polígonos
La suma de la medida en grados de los ángulos interiores de un polígono es igual a 180 (n - 2), donde n representa el número de lados.
La suma de los ángulos exteriores de un polígono es 360 # 176-.
El área de un polígono regular es igual
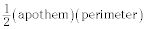
los apotema es el segmento de línea desde el centro del polígono al punto medio de uno de los lados.
Coordinar Fórmulas Geometría
Coordinar la geometría es el estudio de figuras geométricas graficados en un plano de coordenadas. La fórmula de la pendiente se puede utilizar para determinar si las líneas son paralelas o perpendiculares. El punto medio se puede utilizar para determinar si son biantenarios segmentos y también se puede utilizar para encontrar el centro de un círculo. La fórmula de la distancia se puede utilizar para determinar las longitudes de los lados de figuras geométricas.
Reglas de transformación para Geometría Problemas
En coordinar problemas de geometría, hay reglas especiales para ciertos tipos de transformaciones. Para determinar el punto de la imagen al realizar reflexiones, rotaciones, traslaciones y dilataciones, utilice las siguientes reglas:
Reflexiones:
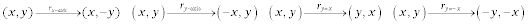
Rotaciones:
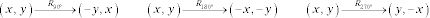
Traducciones:
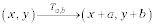
Dilataciones:
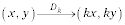
Fundamentos Círculo de Geometría Problemas
Para resolver problemas de geometría sobre círculos, tendrá que conocer los siguientes teoremas círculo involucran tangentes, secantes, y acordes. Estos teoremas se pueden utilizar para encontrar información sobre los ángulos, arcos interceptados y longitud de los segmentos de un círculo. Además, a encontrar la forma estándar y general de un círculo, las fórmulas para el área y el perímetro y el área de un sector de un círculo.
Fórmulas Círculo
La circunferencia de un círculo es igual
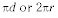
El área de un círculo es igual
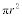
El área de un sector es igual
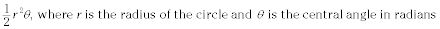
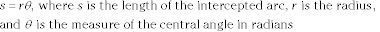
Formulario estándar de un círculo:
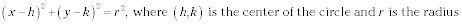
Forma general de un círculo:
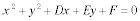
Teoremas Círculo involucran ángulos
El ángulo central es igual a la arco interceptado.
Un ángulo inscrito es igual
Los ángulos verticales interiores formadas por dos acordes de intersección son iguales
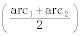
Un ángulo exterior es igual
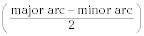
Una línea tangente a un círculo es perpendicular al radio trazado hasta el punto de tangencia.
Teoremas Círculo implican longitudes de segmentos
Cuando una tangente y secante se dibujan desde el mismo punto exterior,
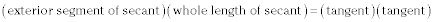
Cuando dos secantes se dibujan desde el mismo punto exterior,
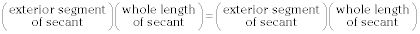
Fórmulas para geométricos sólidos Problemas
Muchas fórmulas están asociados con el estudio de formas tridimensionales en la geometría. Aquí, usted encontrará fórmulas para calcular el volumen, superficie, y el área lateral de cilindros, conos, esferas, pirámides, cubos y prismas rectangulares.
Cilindros
Conos
Esferas
Pirámides cuadradas
Cubos
Prismas rectangulares
Problemas de la práctica de la geometría con triángulos y polígonos
Fórmulas de geometría que usted debe saber
Libro de Geometría para dummies
Cómo una tangente se refiere a un círculo
Cómo calcular el área de un polígono regular
¿Cómo resolver un problema-tangente común
Interior y ángulos exteriores de un polígono
Triángulos trigonométricas básicas
Cómo circunscribir un triángulo
Preparación ASVAB: revisión de geometría
Fórmulas de geometría famosos que usted debe saber para el ASVAB