¿Cómo resolver un problema-tangente común

los problema-tangente común se nombra para el segmento única tangente que es tangente a dos círculos. Su objetivo es encontrar la longitud de la tangente. Estos problemas son un poco complicado, pero deben hacer que poca dificultad si se utiliza el método de solución de tres pasos sencillos que le sigue.

El siguiente ejemplo común implica una externo tangente (donde la tangente se encuentra en el mismo lado de ambos círculos). También puede ser que vea un problema-tangente común que involucra una común interna tangente (donde la tangente se encuentra entre los círculos). No se preocupe: La técnica de solución es la misma para ambos.

Aquí está la manera de resolverlo:

1. Dibujar el segmento que conecta los centros de los dos círculos y sacar los dos radios de los puntos de tangencia (si estos segmentos ya no se han elaborado para usted).

   

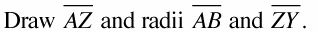
   La siguiente figura muestra este paso. Tenga en cuenta que la distancia dada de 8 entre los círculos es la distancia entre el exterior de los círculos a lo largo del segmento que conecta sus centros.

   

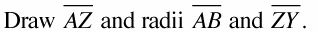
2. Desde el centro de la pequeño círculo, dibujar un segmento paralelo a la tangente común hasta que golpea el radio del círculo más grande (o la extensión del radio en un problema-interno-tangente común).

   Se termina con un triángulo rectángulo y una rectangle- de los lados del rectángulo es la tangente común. La siguiente figura ilustra este paso.

   

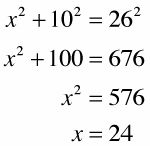
3. Ahora tiene un triángulo rectángulo y un rectángulo y puede terminar el problema con el Teorema de Pitágoras y el simple hecho de que los lados opuestos de un rectángulo son congruentes.

   Hipotenusa del triángulo está formado por el radio del círculo LA, el segmento entre los círculos, y el radio de círculo Z. Sus longitudes suman 4 + 8 + 14 = 26. Se puede ver que el ancho del rectángulo es igual al radio del círculo LA, que es 4 porque los lados opuestos de un rectángulo son congruentes, entonces se puede decir que una de las patas del triángulo es el radio del círculo Z menos 4 o 14-4 = 10. Ahora ya sabe dos lados del triángulo, y si encuentras el tercer lado, que te da la longitud de la tangente común. Usted consigue el tercer lado con el teorema de Pitágoras:

   

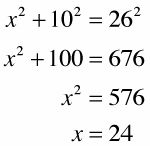
   (Por supuesto, si usted reconoce que el triángulo rectángulo está en el 5: 12: 13 de la familia, usted puede multiplicar 12 por 2 para obtener 24 en vez de usar el Teorema de Pitágoras.)

   Debido a que los lados opuestos de un rectángulo son congruentes, POR es también de 24 años, y ya está.

Ahora mirar hacia atrás en la última cifra y nota donde los ángulos rectos son y cómo el triángulo rectángulo y el rectángulo son situated- a continuación, asegúrese de prestar atención a lo siguiente consejo y advertencia.

Tenga en cuenta la ubicación de la hipotenusa. En un problema-tangente común, el segmento que conecta los centros de los círculos es siempre la hipotenusa de un triángulo rectángulo. La tangente común es siempre el lado de un rectángulo, no una hipotenusa.

En un problema-tangente común, el segmento que conecta los centros de los círculos es nunca uno de los lados de un ángulo recto. No cometa este error común.