Cómo determinar el área de sectores y segmentos de un círculo
Marque una sección de un círculo con un arco y una cuerda, y usted tiene un segmento (este tipo de segmento tiene nada que ver con un segmento de línea). Lanzar un par de radios alrededor de un arco, y usted tiene un sector.
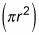
Así que aquí están las definiciones de las dos regiones (La figura de arriba muestra a los dos):
* Sector: Una región limitada por dos radios y un arco de un círculo (definición llanura Inglés: La forma de un pedazo de pizza)
* Segmento de un círculo: Una región limitada por una cuerda y un arco de un círculo
Área de un sector: El área de un sector (por ejemplo, sector PQR en la figura anterior) es igual al área del círculo
veces la fracción del círculo que representa el sector:
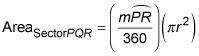
He aquí un ejemplo: el uso de la figura siguiente,
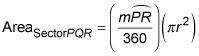
utilizar la fórmula para encontrar el área del sector ACB.
Área de un segmento: Para calcular el área de un segmento como el de la primera figura, simplemente restar el área del triángulo de la zona del sector (por cierto, no hay manera técnica para nombrar segmentos, pero se puede llamar a éste segmento circular XZ):
El problema siguiente ilustra cómo encontrar la longitud del arco, área de sector, y el área del segmento:
Aquí está la solución:
Encuentra la longitud del arco IK.
Usted realmente no necesita una fórmula para encontrar la longitud del arco si usted entiende los conceptos:
Eso es todo al respecto. Así es como todo esto se ve cuando usted lo enchufa en la fórmula:
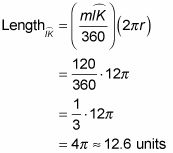
Encuentre el área de sector IDK.
Un sector es una fracción del área del círculo. Porque 120 # 176- ocupa un tercio de los grados en un círculo, el sector IDK ocupa un tercio de la superficie del círculo. Aquí está la solución formal:
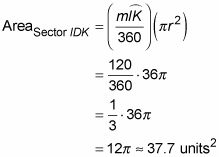
Encuentre el área de segmento circular IK.
Para encontrar el área del segmento, lo que necesita el área del triángulo IDK por lo que puede restar de la zona del sector IDK. Dibuja una altitud hacia abajo desde D para segmentar IK. Eso crea dos 30 # 176-- 60 # 176-- 90 # 176- triángulos.
Usted está todo listo para terminar con la fórmula del área del segmento:
-
Mida la longitud y personalizar escala en la TI-Nspire -
Conceptos de geometría a su estudiante de la escuela secundaria deben conocer las normas básicas comunes -
¿Cómo medir los círculos -
Encontrar el área de una superficie de revolución -
1.001 problemas de la práctica de la geometría para los maniquíes -
Determinar el área de un triángulo desde su base y la altura
Cómo calcular el área de un hexágono regular Una forma de encontrar el área de un hexágono regular es de primera división en triángulos equiláteros. También es necesario utilizar un apotema - un segmento que une el centro de un polígono regular hasta el punto medio de cualquier lado y…
Cómo calcular el área de un polígono regular LA polígono regular es equilátero (tiene lados iguales) y equiangular (tiene ángulos iguales). Para encontrar el área de un polígono regular, se utiliza un apotema - un segmento que une el centro del polígono al punto medio de cualquier lado y…
Cómo calcular el área de un cometa Usted calcula el área de un cometa mediante el uso de las longitudes de sus diagonales. He aquí un ejemplo: ¿cuál es el área de la cometa COMETA en la siguiente figura?Para los problemas de la cometa zona (y algunas veces otros problemas…
Cómo calcular el área de un trapecio Usted puede utilizar el derecho; truco triángulo para encontrar el área de un trapecio. La siguiente trapezoide TRAP parece un trapecio isósceles, ¿no? No se olvide - las apariencias engañan.Usted debe estar pensando, triángulos rectángulos,…
Cómo determinar la longitud de un arco La longitud de un arco significa la misma longitud que el sentido común siempre significa - usted sabe, al igual que la longitud de un trozo de cuerda (con un arco, por supuesto, sería una pieza curvada de cadena). Asegúrese de no mezclar hasta…
Cómo identificar radios, acordes, y diámetros Cuando se trabaja con los círculos, hay tres componentes en línea recta que tiene que ser capaz de identificar: radios, acordes, y diámetros.Radio: El radio de un círculo - la distancia desde su centro a un punto en el círculo - le dice el…
Cómo utilizar radios extra para resolver un problema Al comprar una casa, las tres cosas más importantes a considerar son localización, localización, localización. Con los círculos, es radios, radios, radios. En los problemas de círculo, a menudo es necesario añadir radios extra y radios…
Ángulos en un círculo Hay varias maneras de dibujo un ángulo en un círculo, y cada uno tiene una forma especial de calcular el tamaño de ese ángulo. Cuatro tipos diferentes de ángulos son: central, inscrito, interior, y exterior. Aquí, verá ejemplos de estos…
Acordes frente tangentes de los círculos Usted muestra el diámetro y el radio de un círculo dibujando segmentos a partir de un punto en el círculo, ya sea hacia oa través del centro del círculo. Sin embargo, otras dos figuras rectas tienen un lugar en un círculo. Una de estas figuras…
Cómo localizar el centro de un círculo Una forma de describir el centro de un círculo es identificar la centroide. Este punto medio es el centro de gravedad, donde se puede equilibrar el triángulo y girar a su alrededor.Al graficar un círculo, triángulo, o segmento de línea mediante…
Cómo relacionarse radianes a exploraciones de radar La mayor ventaja de utilizar radianes en lugar de grados es que un radián está directamente relacionado con una longitud - la longitud o distancia alrededor de un círculo, que se llama su circunferencia. Usando radianes es muy útil cuando…
Cómo utilizar radianes para resolver un problema trig Usando radianes es muy útil cuando usted está haciendo aplicaciones de trigonometría que implican la longitud de un arco de un círculo, que es parte de su circunferencia. Esto podría incluir la medición de la barrida de una mano en un reloj o…