Fórmulas geométricas que usted debe saber para el examen de la base praxis
Usted tendrá que saber fórmulas geométricas para el Examen Praxis Core. Las figuras geométricas tienen ciertas propiedades, y el número de dimensiones que tienen es parte de lo que decide qué otras propiedades que tienen. Los segmentos de línea tienen una distancia que se puede denominar como la longitud, anchura, o la altura.
Figuras bidimensionales como círculos y triángulos tienen zona, así como las piezas con las mediciones unidimensionales. Figuras geométricas tridimensionales tienen las propiedades anteriores, más volumen. Las fórmulas no se proporcionan en la Praxis Core, por lo que usted necesita saber las principales fórmulas de área, área de superficie y volumen.
Perímetro
El perímetro de una figura bidimensional es la distancia alrededor de ella. Para determinar el perímetro de un polígono, puede agregar todas las medidas laterales. La siguiente rectángulo tiene un perímetro de 28 metros.
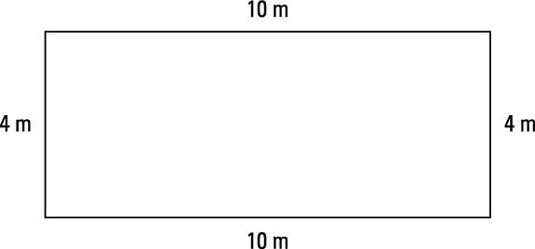
Debido a que los lados opuestos de un rectángulo son congruentes, una fórmula hace que el cálculo del perímetro más simple que la suma de todas las medidas secundarios. Dos de los lados tienen la longitud (l), Y dos lados tienen la anchura (w), Por lo que la adición de dos veces la longitud y el doble de la anchura da el perímetro:
Perímetro del rectángulo = 2l + 2w
Debido a que la longitud y la anchura de un cuadrado son los mismos, se puede obtener el perímetro multiplicando la medida de un lado por 4.
Circunferencia
El perímetro de un círculo es el círculo de circunferencia. La fórmula para la circunferencia implica # 960-, que es la relación de la circunferencia de un círculo (C) Dividido por su diámetro (d). Debido a que todos los círculos son similares, la relación es la misma para todos los círculos.
# 960- es un número irracional, así que nunca termina o las repeticiones en forma decimal, pero su valor puede ser redondeado a 3,14. Debido a la circunferencia dividida por el diámetro es # 960-, la circunferencia es momento de diámetro # 960-:
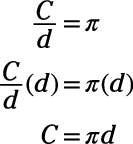
El diámetro de un círculo es dos veces el radio, por lo d = 2r. Por Consiguiente, C = # 960- (2r). La manera formal a escribir un término es con los números antes de variables y 960- # es un número, por lo que la fórmula oficial de la circunferencia es la siguiente:
C = 2 # 960-r
Recuerde que dentro de una fórmula, cualquier variable se puede representar a un desconocido en un problema. Para encontrar el valor de la variable, llenar cada número conocido en la fórmula y resuelve para lo que aún no se conoce.
¿Cuál es el radio de un círculo con una circunferencia de 10 # 960- unidades?
(A) 10
(B) 5
(C) 100
(D) 5 # 960;
(E) 10 # 960;
La respuesta correcta es la opción (B). Puede utilizar la fórmula para la circunferencia y resolver r.
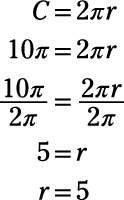
Las otras opciones son el resultado de mal uso de la fórmula de la circunferencia o el uso de la fórmula equivocada.
Si recibir la respuesta a una pregunta implica el uso de una fórmula con # 960- en el mismo, # 960- no puede aparecer como parte de las opciones de respuesta. En ese caso, es necesario utilizar 3.14, a la aproximación de # 960- y hacer el cálculo.
Area
Una figura de dos dimensiones existe en un plano. El área de una figura bidimensional es la cantidad de avión en ella. En otras palabras, el área es una medida de cuánto espacio está dentro de una forma de dos dimensiones. Diferentes formas tienen diferentes fórmulas del área.
El área de un paralelogramo es su base veces su altura. La base puede ser cualquiera de los lados, pero la altura tiene que ser la medida de un segmento que es perpendicular a la misma y su lado opuesto.
área de paralelogramo = bh
El área de la siguiente paralelogramo es su base por su altura, o (7 cm) (10 cm) o 70 cm2.
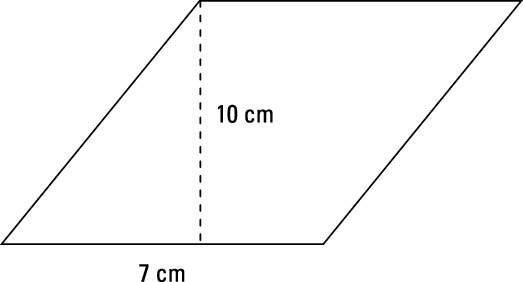
Cualquier combinación de la base y la altura de un rectángulo, que es un tipo de paralelogramo, es una combinación de longitud (l) Y anchura (w), Por lo que el área de un rectángulo es lw. Los cuatro lados de un cuadrado son congruentes por lo que todo lo que tienes que hacer es multiplicar una medida de lado a sí mismo.
Si un paralelogramo se corta en los vértices, el resultado es dos triángulos congruentes. También, cualquier triángulo se puede poner junto con un triángulo congruente para formar un paralelogramo. Debido a esto, cada triángulo tiene la mitad del área del paralelogramo que se puede formar poniendo el triángulo con una copia exacta de sí mismo. Por lo tanto, el área de un triángulo no es la base por la altura, pero un medio que:
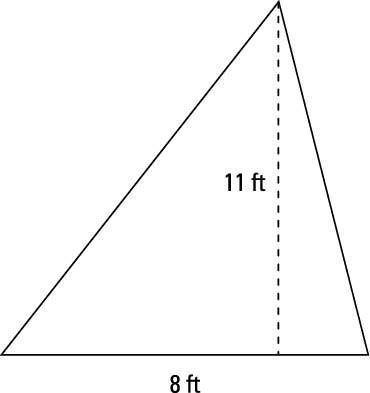
El área de la siguiente triángulo es 1 / 2BH, o medio (8 pies) (11 pies), que es de 44 ft2.
Asegúrese de conocer las fórmulas para encontrar las áreas de figuras comunes así porque probablemente le pedirá al menos una pregunta sobre el área en la Praxis.
| Cifra | Area |
|---|---|
| Paralelogramo | bh |
| Rectángulo | lw |
| Cuadrado | s2 |
| Triángulo | 1 / 2BH |
| Círculo | et-r2 |
Encontrar el volumen correcto
El volumen es una medida tridimensional. Mientras que el área de superficie es la cantidad de plano sobre la superficie de una figura tridimensional, el volumen es la cantidad de espacio dentro de una figura tridimensional. Para sólidos rectangulares y cilindros, el volumen se puede encontrar multiplicando el área de la base por la altura.
Para sólidos rectangulares, el volumen se lwh más específicamente desde lw es el área de la base. El volumen de una pirámide es un tercio lo que el volumen sería si los ápice eran una base congruentes en lugar de un punto, y un cono es 1/3 del volumen de lo que sería si los ápice eran una base congruentes en lugar de una punto.
Es por eso que el volumen de una pirámide o de cono es 1 / 3Bh lugar de Bh. Recuerde que las bases de los conos y cilindros son círculos.
La altura de una de estas figuras es la medida de un segmento que va desde un vértice o una base perpendicular al plano en el que la base, u otra base, mentiras. Si usted tiene alguna duda sobre estas cifras en el examen Praxis Core, la altura más probable es que la medida de un segmento que es perpendicular a la base real. Los segmentos de puntos representan la altura.
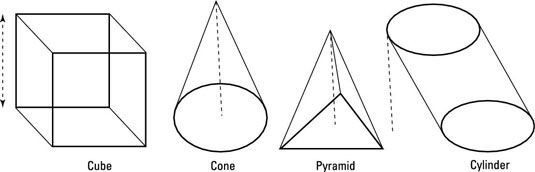
Echa un vistazo a las fórmulas para los volúmenes de las principales figuras tridimensionales.
| Cifra | Volumen |
|---|---|
| Sólido rectangular | Bh o lwh |
| Cilindro | et-r2h |
| Pirámide | 1 / 3Bh |
| Cono | 1 / 3eth-r2h |
| Esfera | 4 / 3eth-r3 |






