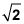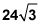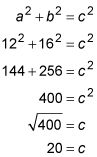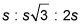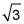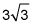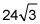Preguntas de práctica geometría plana en el acto
Varias de las preguntas en el examen de matemáticas ACT cubrir geometría plana (lo que piensan como "figuras apenas llano", como triángulos, círculos, cuadriláteros, y así sucesivamente). Aquí hay un par de preguntas para ayudarle a empezar.
Ejemplos de preguntas
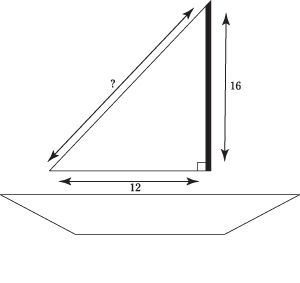
Un barco de vela tiene una vela que es de 16 pies de alto. La base de la vela mide 12 pies. ¿Cuál es la medida en pies desde el punto inferior izquierda de la base de la vela a la parte superior de la vela?
(LA) 18
(B) 19
(C) 20
(D)
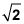
(E) 28
Janet está llenando en un parche de césped con césped. El parche se encuentra en la forma de un paralelogramo. La longitud del parche es de 8 pies y su anchura es de 6 pies. Uno de los ángulos interiores mide 120 grados. ¿Cuántos pies cuadrados de césped se Janet necesita para llenar completamente el parche?
(F) 48
(G)
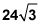
(H)

(J) 24
(K) 18
Respuestas y explicaciones
1. La respuesta correcta es la opción (C).
El problema le dice que la altura de la vela es perpendicular a su base, lo que significa que la vela se forma un triángulo rectángulo. La pregunta le pide que encontrar la medida de la hipotenusa de ese triángulo. Antes de llamar a Pitágoras y su teorema, comprobar la relación entre el triángulo. Es 12:16:X. Observe que 12 es 4 veces 3 y 16 es 4 veces 4. Parece un 3: triángulo rectángulo 5: 4! Multiplique 5 por 4 para completar la proporción. La respuesta tiene que ser de 20, que es opción (C). Si elige cualquier otra respuesta, que se acaba de adivinar.
Si se olvida de las relaciones comunes de triángulos rectángulos, puede confiar en el teorema de Pitágoras para encontrar la medida. El teorema afirma que la hipotenusa al cuadrado es igual a la suma de los cuadrados de los otros lados: la2 + b2 = c2. Conecte las dos longitudes de los lados y resuelve para c:
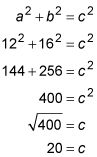
2. La respuesta correcta es la opción (G).
El número de pies cuadrados de césped es el área del paralelogramo. El área de un paralelogramo es bh. La base del jardín es la longitud de uno de sus lados (dicen los uno mide 8 pies de largo.) Debido a que el jardín tiene la forma de un paralelogramo, no se puede asumir que la medida de su ancho es de los 6 pies miden en el otro lado. Para encontrar la medida de ancho, dibujar un paralelogramo que se inclina hacia la derecha y crear un triángulo rectángulo dibujando una línea desde la esquina superior izquierda que es perpendicular a la base.
El ángulo de su nueva línea se extiende desde mide 120 grados. Los ángulos opuestos en un paralelogramo tienen las mismas medidas, y los cuatro ángulos suman 360 grados. Eso significa que los dos ángulos más pequeños de la medida de jardín 60 grados y el otro ángulo grande mide 120 grados.
El triángulo rectángulo que has creado es un triángulo rectángulo 30:60:90. La relación de lado de un triángulo es 30:60:90
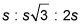
El lado más pequeño (el opuesto al ángulo de 30 grados) es igual a la mitad de la hipotenusa, y el lado más largo (el opuesto al ángulo de 60 grados) es igual a la parte más pequeña multiplicado por
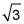
La parte más pequeña es la mitad de 6, que es 3, y el lado más largo, la altura del paralelogramo, es
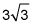
Multiplique ese valor por la base de 8. El número de pies cuadrados de césped que necesita Janet es
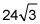
Sobre el autor
 Descubriendo ternas pitagóricas
Descubriendo ternas pitagóricas El teorema de Pitágoras es sin duda uno de los teoremas más famosos de toda la matemática. Matemáticos y laicos por igual han estudiado durante siglos, y la gente ha demostrado de muchas maneras diferentes. (Incluso el presidente James Garfield…
 Geometría fórmulas y reglas para triángulos
Geometría fórmulas y reglas para triángulos Las pirámides de tres ángulos, bidimensionales conocidos como triángulos son uno de los componentes básicos de la geometría (sin embargo de tres picos que sean). Triángulos, por supuesto, tienen sus propias fórmulas para encontrar el área y…
 Problemas de la práctica de la geometría con triángulos y polígonos
Problemas de la práctica de la geometría con triángulos y polígonos LA polígono es una figura geométrica que tiene al menos tres lados. El triángulo es el polígono más básico. Usted encontrará las siguientes fórmulas y propiedades útiles al responder a las preguntas que implican desigualdades triángulo,…
 Cómo calcular el área de un paralelogramo, cometa, o trapezoidal
Cómo calcular el área de un paralelogramo, cometa, o trapezoidal Las fórmulas del área para el paralelogramo, cometa, y trapezoide se basan en el área de un rectángulo. Las siguientes figuras muestran cómo cada uno de estos tres cuadriláteros se refiere a un rectángulo, y la siguiente lista te da los…
 Identificar escaleno, isósceles y triángulos equiláteros
Identificar escaleno, isósceles y triángulos equiláteros Los triángulos se clasifican según la longitud de sus lados o la medida de sus ángulos. Estas clasificaciones vienen de tres en tres, al igual que los lados y ángulos de sí mismos.Las siguientes son las clasificaciones de triángulos basada en…
 La identificación de triángulos por sus ángulos
La identificación de triángulos por sus ángulos Se puede clasificar triángulos por sus ángulos, así como por sus lados. Las clasificaciones basadas en ángulos son como sigue:Triángulo aguda: Un triángulo con tres ángulos agudos (menos de 90 # 176-).Triángulo obtuso: Un triángulo con un…
 Propiedades de rombos, rectángulos y cuadrados
Propiedades de rombos, rectángulos y cuadrados Los tres paralelogramos especiales - rombo, rectángulo y cuadrado - son los llamados porque son casos especiales del paralelogramo. (Además, la plaza es un caso especial o escribe tanto del rectángulo y rombo.)La jerarquía de tres niveles que se…
 Triángulos trigonométricas básicas
Triángulos trigonométricas básicas Todo por su cuenta, los ángulos son sin duda muy emocionante. Pero los puso en un triángulo, y usted tiene la guinda del pastel. Triángulos son una de las figuras geométricas estudiadas con más frecuencia. Los ángulos que forman el triángulo…
 La determinación de si un objeto largo encaja en una esquina pasillo
La determinación de si un objeto largo encaja en una esquina pasillo Aquí hay una aplicación de la trigonometría que puede muy bien ser capaz de relacionarse con: ¿Alguna vez ha tratado de conseguir un mueble grande en una esquina en una casa? Usted girar y girar y lo puso de punta, pero fue en vano. En este…
 Cómo determinar la altura de un árbol
Cómo determinar la altura de un árbol ¿Qué función trigonométrica se debe utilizar para determinar la altura de un árbol? Supongamos que usted está volando una cometa, y se ve atrapado en la parte superior de un árbol. Has dejado a cabo los 100 pies de cadena para el kite, y el…
 La función coseno: adyacente sobre la hipotenusa
La función coseno: adyacente sobre la hipotenusa La función trigonométrica coseno, abreviado cos, funciona mediante la formación de esta relación: adyacente / hipotenusa. En la figura, se ve que los cosenos de los dos ángulos son los siguientes:La situación con las proporciones es el mismo…
 Preparación ASVAB: revisión de geometría
Preparación ASVAB: revisión de geometría Usted tendrá que tener un conocimiento básico de la geometría para el ASVAB. Geometry es ". La rama de las matemáticas que se ocupa de la deducción de las propiedades, la medición, y las relaciones de puntos, líneas, ángulos y figuras en el…