¿Cómo encontrar el volumen de una forma utilizando el método de la arandela de la integración
Geometría te dice cómo calcular los volúmenes de sólidos sencillos. Integración que permite calcular los volúmenes de una infinita variedad de formas mucho más complicadas. Si usted tiene una forma circular con un agujero circular en el centro, se puede utilizar el método de la lavadora para encontrar su volumen mediante la reducción de la forma en trozos delgados y luego sumar los volúmenes de las rodajas. No hay nada a ella.
Aqui tienes.
y generar un sólido mediante la revolución de esa zona de la X-eje.

Basta pensar: Todas las fuerzas del universo en evolución y todos los giros y vueltas de su vida que han llevado a este momento en que usted es finalmente capaz de calcular el volumen de esta forma de tazón raro - algo para su diario. ¿Cuál es el volumen?
Determinar donde las dos curvas se cruzan.

Así el sólido en cuestión se extiende por el intervalo en el X-eje de 0 a 1.
Figura el área de una arandela de sección transversal.

La cifra inmediatamente superior muestra una sección transversal típica de la forma 3-D, pero resultó lo que estás mirando de frente. Cada rebanada tiene esta forma la arandela por lo que su área es igual al área de todo el círculo menos el área del agujero.
El área del círculo menos el agujero es
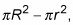
dónde R es el radio exterior (el gran radio) y r es el radio del agujero (el pequeño radio).
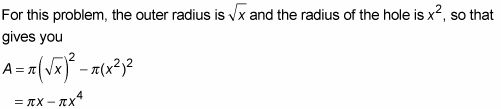
Multiplique esta área por el grosor, dx, para obtener el volumen de una arandela representativo.
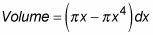
Sume los volúmenes de las arandelas de 0 a 1 mediante la integración.
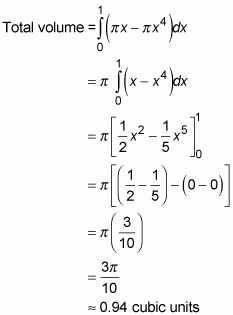
Foco en el simple hecho de que el área de una lavadora es el área de todo el disco,
menos el área del agujero,
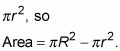
Mediante la integración, se obtiene
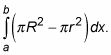
Este es el mismo, por supuesto, como
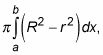
que es la fórmula que se da en la mayoría de los libros. Pero si usted acaba de aprender que de memoria, es posible que se olvide de ella. Es más probable que recordar cómo hacer estos problemas si se entiende la idea simple de gran círculo de-menos-poco-círculo.






