La medición de volumen bajo una superficie usando una integral doble
Una integral doble le permite medir el volumen bajo una superficie tan limitada por un rectángulo. Integrales definidas proporcionan una forma confiable de medir el área firmado entre una función y la X-eje como limitada por cualquiera de los dos valores de X. Del mismo modo, una doble integral le permite medir el volumen firmado entre una función z = F(X, y) y el xy-plano que delimitada por cualquiera de los dos valores de X y cualquiera de los dos valores de y.
He aquí un ejemplo de una integral doble:
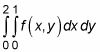
Aunque pueda parecer complicado, una integral doble es realmente una integral dentro de otro integrante. Para ayudarle a ver esto, la integral interior en el ejemplo anterior se encuentra entre corchetes fuera aquí:
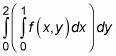
Cuando te enfocas en la integral dentro de los corchetes, se puede ver que los límites de integración para 0 y 1 corresponden con el dx - eso es, X = 0 y X = 1. De manera similar, los límites de integración 0 y 2 se corresponden con las dy - eso es, y = 0 y y = 2.
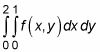
Esta figura muestra lo que este volumen se parece. Las medidas integrales dobles del volumen entre F(X, y) y el xy-plano que delimitada por un rectángulo. En este caso, el rectángulo es descrito por las cuatro líneas X = 0, X = 1, y = 0, y y = 2.
Encontrar la integral de un producto de dos funciones A veces la función que usted está tratando de integrar es el producto de dos funciones - por ejemplo, el pecado3 X y cos X. Sería lo más sencillo diferenciar con la regla del producto, pero la integración no tiene una regla del producto.…
Encuentra la integral de funciones anidadas A veces es necesario integrar una función que es la composición de dos funciones - por ejemplo, la función 2X anidada dentro de una función seno. Si estaba diferenciando, se puede utilizar la regla de la cadena. Desafortunadamente, no existe una…
¿Cómo funciona la integración: es sólo Además de lujo El significado más fundamental de la integración es sumar. Y cuando representas la integración en un gráfico, se puede ver el proceso de sumar como un resumen de finas tiras rectangulares de área para llegar al área total bajo la curva, como…
Cómo evaluar una integral impropia que es horizontalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA horizontalmente infinita integral impropia contiene ya sea # 8734- o - # 8734- (o ambos) como un límite de la integración.Evaluación de una integral impropia es un…
Cómo evaluar una integral impropia que es verticalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…
¿Cómo encontrar el volumen de un sólido entre dos superficies de revolución Si desea encontrar el volumen de un sólido que se encuentra entre dos superficies distintas de la revolución, puede utilizar el método de carne máquina de cortar para hacer esto. los Método de carne máquina de cortar funciona mejor con los…
Cómo medir el volumen de un sólido de forma irregular Se puede medir el volumen de cualquier sólido con una sección transversal que es una función de de forma irregular X. En algunos casos, estos sólidos son más difíciles de describir de lo que son para medir. Por ejemplo, echar un vistazo a esta…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver integrales impropias de funciones que tienen asíntotas verticales A resolver integrales impropias, al convertirlos en problemas de límite. No se puede hacer de ellos la manera regular. He aquí cómo resolver integrales impropias de funciones que tienen asíntotas verticales. Hay dos casos: una asíntota vertical…
¿Cómo resolver integrales impropias que tienen uno o dos límites infinitos de integración Una de las formas en que pueden ser integrales definidas inadecuada es cuando uno o ambos de los límites de integración son infinitas. A resolver este tipo de integral impropia al convertirlo en un problema de límite en c tiende a infinito o…
Cómo dividir una integral definida en dos integrales definidas Cuando la solución de problemas de la zona, a veces es necesario dividir una integral en dos integrales definidas separadas. Aquí hay una regla simple, pero muy útil para hacer esto que parece complicado, pero es realmente muy fácil:Esta regla…
Cómo utilizar el método Shell para medir el volumen de un sólido los método de shell permite medir el volumen de un sólido mediante la medición del volumen de muchas superficies concéntricas de volumen, llamado " conchas ". Aunque el método de shell funciona sólo para sólidos con secciones transversales…