¿Cómo resolver integrales impropias de funciones que tienen asíntotas verticales
A resolver integrales impropias, al convertirlos en problemas de límite. No se puede hacer de ellos la manera regular. He aquí cómo resolver integrales impropias de funciones que tienen asíntotas verticales. Hay dos casos: una asíntota vertical puede estar en el borde de la zona de que se trate o en el centro de la misma.
Conteúdo
Caso I: La función tiene una asíntota vertical en uno de los límites de la integración
¿Cuál es el área bajo
de 0 a 1? Esta función no está definida para X = 0, y tiene una asíntota vertical allí. Así que tienes que girar la integral definida en un límite:
Esta área es infinita, lo que probablemente no le sorprendió porque la curva sube hasta el infinito. Pero aferrarse a su sombrero, a pesar del hecho de que la siguiente función también sube hasta el infinito en X = 0, su área es finito!
Encuentra el área bajo
de 0 a 1. Esta función también está definido en X = 0, por lo que el proceso es el mismo que en el ejemplo anterior.
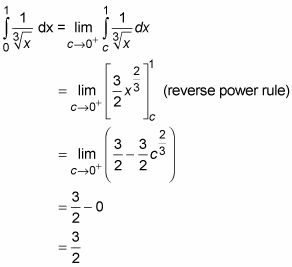
Convergencia y Divergencia: Usted dice que una integral impropia converge si existe el límite, es decir, si el límite es igual a un número finito como en el segundo ejemplo. De lo contrario, se dice que una integral impropia a divergir - al igual que en el primer ejemplo.
Caso II: La función tiene una asíntota vertical entre los límites de integración
Si el punto del integrando indefinido es en algún lugar entre los límites de integración, permite dividir la integral en dos, - en el punto indefinido - a continuación, convertir cada integrante en un límite e ir de allí.
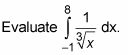
Este integrando no está definido en X = 0.
Dividir la integral en dos en el punto definido.
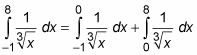
Gire cada integrante en un límite y evaluar.
Tenga en cuenta que si usted no puede darse cuenta de que un integrante tiene un punto indefinido entre los límites de la integración, y permite integrar la vía ordinaria, puede obtener la respuesta equivocada. El problema anterior,
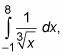
pasa a funcionar bien si lo haces de la manera ordinaria. Sin embargo, si lo hace
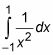
la forma ordinaria, no sólo usted consigue la respuesta equivocada, se obtiene la respuesta totalmente absurdo de negativo 2, a pesar del hecho de que la función es positiva desde -1 a 1. La moral: No se arriesgue.
Si bien parte de la divide integral diverge, los integral diverge originales. Usted no puede conseguir, por ejemplo, el infinito negativo para una parte y el infinito de la otra parte y sumarlos para obtener cero.
-
10 Cosas para recordar acerca de la integración y cálculo -
Libro de Cálculo para dummies -
La determinación de si una serie converge utilizando la prueba de comparación integral - Evaluación de límites en el cálculo
-
La evaluación de las integrales dobles -
Encuentra las zonas exactas bajo una curva mediante la integral definida
Encuentra el área bajo más de una función A veces, una sola área geométrica es descrito por más de una función. Por ejemplo, supongamos que desea encontrar el área sombreada que se muestra en la siguiente figura, el área bajo y = Sen X y y = Cos X de 0 a Pi-/ 2:La primera cosa a notar…
Cómo evaluar una integral impropia que es horizontalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA horizontalmente infinita integral impropia contiene ya sea # 8734- o - # 8734- (o ambos) como un límite de la integración.Evaluación de una integral impropia es un…
Cómo evaluar una integral impropia que es verticalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…
¿Cómo encontrar extremos absolutos sobre todo el dominio de una función Una función de absoluta max y absoluta min sobre su todo el dominio son los valores más altos y más bajos (alturas) de la función de cualquier lugar que está definido. Cuando se tiene en cuenta todo el dominio de una función, una función…
¿Cómo encontrar el límite de una función gráfica Cuando se te da la gráfica de una función y su profesor de pre-cálculo le pide que encontrar el límite, usted lee los valores de la gráfica - algo que has estado haciendo desde que usted aprendió lo que era un gráfico! Si usted está buscando…
¿Cómo resolver un problema de límite de plug-and-chu Algunos problemas de límite, como los problemas de plug-and-chug, son muy fáciles de resolver. Sólo tiene que conectar el número de flecha en la función de límite, y si los resultados de cálculo de un número, esa es su respuesta (pero ver la…
¿Cómo resolver integrales impropias que tienen uno o dos límites infinitos de integración Una de las formas en que pueden ser integrales definidas inadecuada es cuando uno o ambos de los límites de integración son infinitas. A resolver este tipo de integral impropia al convertirlo en un problema de límite en c tiende a infinito o…
¿Cómo resolver los límites en el infinito con una calculadora Despejando límites en el infinito es fácil de hacer cuando se utiliza una calculadora. Por ejemplo, escribir la función debajo en el modo de gráficos de la calculadora:entonces ve a tpoder setup y establecer TblStart a 100.000 y # 8710-Tbl a…
¿Cómo resolver los límites en el infinito mediante el uso de asíntotas horizontales Asíntotas horizontales y límites en el infinito siempre van de la mano. No se puede tener uno sin el otro. Si usted tiene una función racional comodeterminar el límite en el infinito o infinito negativo es lo mismo que encontrar la ubicación de…
Cómo dividir una integral definida en dos integrales definidas Cuando la solución de problemas de la zona, a veces es necesario dividir una integral en dos integrales definidas separadas. Aquí hay una regla simple, pero muy útil para hacer esto que parece complicado, pero es realmente muy fácil:Esta regla…
Límites y continuidad en pre-cálculo En matemáticas, una límite sugiere que usted está acercando a un cierto valor. Algunas funciones, tales como una función racional con una asíntota horizontal, tienen un límite como el X los valores se mueven hacia el infinito positivo o…
La medición de volumen bajo una superficie usando una integral doble Una integral doble le permite medir el volumen bajo una superficie tan limitada por un rectángulo. Integrales definidas proporcionan una forma confiable de medir el área firmado entre una función y la X-eje como limitada por cualquiera de los dos…