Encuentra las zonas exactas bajo una curva mediante la integral definida

Cuando se aproxima el área bajo una curva utilizando rectángulos, los más rectángulos que utiliza la izquierda, derecha, o punto medio, mejor será la aproximación. Por lo tanto, "todos" que tendría que hacer para conseguir el área exacta bajo una curva es utilizar un número infinito de rectángulos. Ahora, realmente no se puede hacer eso, pero con la invención fantástica de los límites, esto es una especie de lo que sucede. Aquí está la definición de la integral definida que se utiliza para calcular las zonas exactas.

los integral definida ("sencillo" la definición):El área bajo una curva exacta entre X = la y X = b está dada por la integral definida, que se define como el límite de una suma de Riemann:

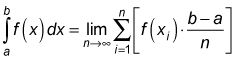
¿Eso es una cosa de belleza o qué? Tenga en cuenta que esta suma (todo a la derecha de "lim") es idéntica a la fórmula para n rectángulos derecha, R_n:

La única diferencia es que se toma el límite de esa fórmula como el número de rectángulos tiende a infinito

Esta definición de la integral definida es la versión simple basado en la fórmula rectángulo derecha. Verá la definición real McCoy en un momento, sino porque todas las sumas de Riemann para un problema específico tienen el mismo límite - en otras palabras, no importa qué tipo de rectángulos se utiliza - que también podría utilizar el derecho; definición rectángulo. Es lo menos complicado y que siempre va a bastar.

Esta es el área exacta bajo F (X) = X² + 1 entre X = 0 y X = 3:

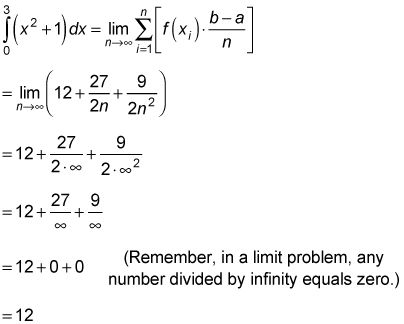
Gran sorpresa.

Este resultado es bastante sorprendente si se piensa en ello. Utilizando el proceso de límite, se obtiene una exacto respuesta de 12 - algo así como 12,00000000 ... a un número infinito de decimales - por el área bajo la función suave, curva F (X) = X² + 1, basándose en las áreas de rectángulos de cima plana que se ejecutan a lo largo de la curva en una, la moda de diente de sierra dentada.

Encontrar el área exacta de 12 utilizando el límite de una suma de Riemann es un montón de trabajo (recuerde, usted primero tiene que determinar la fórmula para n rectángulos derecha). Este complicado método de integración es comparable a la determinación de un derivado de la forma más dura con la definición formal que se basa en el cociente de diferencias.

Debido a que el límite de todas las sumas de Riemann es el mismo, los límites en el infinito de n rectángulos izquierdo y n rectángulos punto medio - para F (X) = X² + 1 entre X = 0 y X = 3 - que debe dar el mismo resultado que el límite en el infinito de n rectángulos derecha. Aquí está el límite rectángulo izquierda:

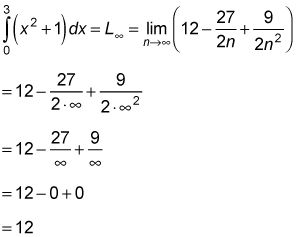
Y aquí está el límite rectángulo punto medio:

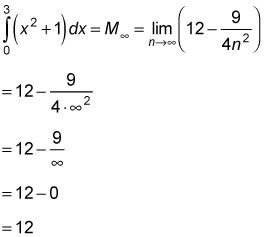
Si usted es un tanto incrédula que estos límites en realidad te la dan exacto área bajo F (X) = X² + 1 entre 0 y 3, usted no está solo. Después de todo, en estos límites, como en todos los problemas de límite, el número de la flecha

es solo acercado- que es en realidad nunca llegó. Y encima de eso, ¿qué significaría para alcanzar el infinito? No puede hacerlo. Y sin importar cuántos rectángulos que usted tiene, usted siempre tiene que, con el borde de diente de sierra dentada. Entonces, ¿cómo puede un procedimiento de este tipo le dará el área exacta?

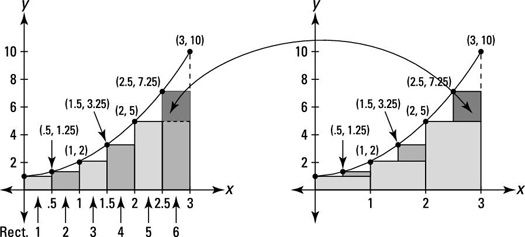
Míralo de esta manera. Echa un vistazo a las siguientes dos cifras.

f (X) = X² + 1 ". />

Se puede decir de estas cifras que la suma de las áreas de rectángulos izquierda, independientemente de su número, siempre será un bajoestimar (este es el caso para las funciones que están aumentando en el lapso en cuestión).

Y a partir de la siguiente figura, se puede ver que la suma de las áreas de rectángulos correctas, independientemente de la cantidad que usted tiene, siempre será una encimaestimar (por el aumento de funciones).

Por lo tanto, debido a que los límites en el infinito de la subestimación y la sobreestimación son ambos iguales a 12, que debe ser el área exacta. (Un argumento similar trabaja para disminuir las funciones.)

Todas las sumas de Riemann para un problema dado tienen el mismo límite. No sólo son los límites en el infinito de la izquierda, rectángulos derecha, y el punto medio de la misma para un problema dado, el límite de la suma de Riemann también le da la misma respuesta. Usted puede tener una serie de rectángulos con desigual widths- usted puede tener una mezcla de izquierda, derecha, y rectangles- punto medio o puede construir los rectángulos para que toquen la curva en otro lugar que en sus esquinas superiores izquierda o derecha, o en los puntos medios de sus lados superiores. Lo único que importa es que, en el límite, la anchura de todos los rectángulos tiende a cero (y de aquí se desprende que el número de rectángulos tiende a infinito). Esto le lleva a la siguiente hacia abajo y sucio jumbo totalmente extrema, Mumbo integración que toma todas estas posibilidades en cuenta.

los integral definida (McCoy real definición): La integral definida de

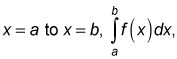
es el número al que todas las sumas de Riemann tienden como la anchura de todos los rectángulos tiende a cero y, como el número de rectángulos se aproxima al infinito:

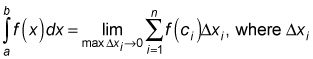
es la anchura de la yoTH rectángulo y c_yo es el X-de coordenadas del punto donde el yotoques rectángulo th F (X). (Ese

simplemente garantiza que la anchura de todos los rectángulos se aproxima a cero y que el número de rectángulos se aproxima al infinito.)