Cómo utilizar la notación sigma para encontrar el área bajo una curva

Puede usar la notación sigma para escribir la suma de Riemann para una curva. Esto es útil cuando se quiere derivar la fórmula para el área aproximada bajo la curva. Por ejemplo, digamos que usted desea encontrar el área aproximada de n rectángulos correctas entre X = 0 y X = 3 bajo la función F (X) = X² + 1.

Por cierto, no es necesario la notación sigma para la matemáticas que sigue. Es sólo una "conveniencia" - Oh, seguro. Cruza los dedos y esperar que tu profesor decide no cubrir esto. Se pone muy retorcido.

La regla del punto medio: Usted puede aproximar el área exacta bajo una curva entre la y b,

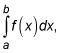
con una suma de rectángulos punto medio dado por la siguiente fórmula. En general, los más rectángulos, mejor será la estimación.

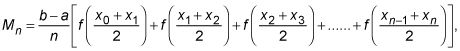
dónde n es el número de rectángulos,

es la anchura de cada rectángulo, X₀ mediante X_n son los n + 1 puntos uniformemente espaciados de la a b, y los valores de la función son las alturas de los rectángulos.

Aplicando la regla del punto medio de este ejemplo, se obtiene:

Aquí está la misma fórmula escrita con la notación sigma:

(Tenga en cuenta que usted podría escribir este lugar como

que más bien reflejar la fórmula anterior donde el

está en el exterior. De cualquier manera está bien - son equivalentes - pero que te pueden optar por mantener la

en el interior de modo que el

suma es en realidad una suma de rectángulos. En otras palabras, con el

en el interior, la expresión después de la

símbolo,

que la

símbolo le indica a sumar, es el área de cada rectángulo, es decir, altura veces base.)

Ahora resolver esto para los seis rectángulos derecha en la figura.

Usted está calculando el área bajo X² + 1 entre X = 0 y X = 3 con seis rectángulos, por lo que la anchura de cada uno,

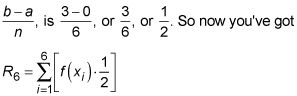
A continuación, debido a que el ancho de cada rectángulo es

los bordes derechos de los seis rectángulos caen en los primeros seis múltiplos de

Estos números son los X-coordenadas de los seis puntos X₁ mediante X₆- que pueden ser generados por la expresión

dónde yo es igual a 1 a 6. Puede comprobar que esto funciona enchufando 1 por yo en

luego 2, luego 3, hasta 6. Así que ahora usted puede reemplazar el X_yo en la fórmula con

dandote

La función en este ejemplo,

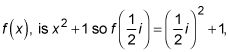
y por lo que ahora se puede escribir

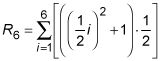
Si enchufa 1 en yo, luego 2, luego 3, y así sucesivamente hasta 6 y hacer los cálculos, se obtiene la suma de las áreas de los rectángulos en la figura. Esta notación sigma es sólo una forma elegante de escribir la suma de los seis rectángulos.

¿Te estas divirtiendo? Espera, se pone peor - lo siento. Ahora usted va a escribir la suma general de un número desconocido, n, rectángulos de la derecha. El lapso total de la zona en cuestión es 3, ¿verdad? Se divide este lapso por el número de rectángulos para obtener el ancho de cada rectángulo. Con 6 rectángulos, la anchura de cada uno es

con n rectángulos, la anchura de cada uno es

Y los bordes derechos de la n rectángulos son generados por

para yo es igual a 1 a través n. Eso te da

O, porque F (X) = X² + 1,

Para este último paso, apretar el

a través de los símbolos de suma - se le permite sacar nada a excepción de una función de yo, la llamada índice de la suma. Además, la segunda sumatoria en el último paso tiene sólo un 1 después de que ni yo. Así que no hay ningún lugar para enchufar los valores de yo. Esta situación puede parecer un poco raro, pero todo lo que hace es sumar n 1s, que es igual a n (esto se hace siguiente).

Ahora ha llegado a una etapa crítica. Con un juego de manos, te vas a convertir esta suma de Riemann en una fórmula en términos de n.

Ahora, ya que casi nadie sabe, la suma de la primera n números cuadrados,

(Por cierto, este 6 no tiene nada que ver con el hecho de que está utilizando 6 rectángulos.) Por lo tanto, puede sustituir esa expresión para el

en la última línea de la solución de la notación sigma, y ​​al mismo tiempo sustituto n para

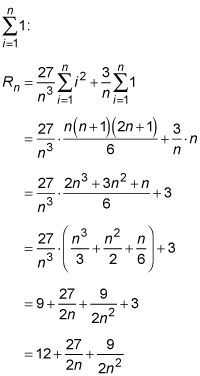
El fin. ¡Finalmente! Esta es la fórmula para el área de n rectángulos correctas entre X = 0 y X = 3 bajo la función F (X) = X² + 1.