10 Cosas para recordar acerca de la integración y cálculo
La integración es una parte fundamental del cálculo. Si quieres convertirte en una persona totalmente integrada (en oposición a un un derivado), integrar estas reglas de integración y hacerlos parte integral de su ser.
Conteúdo
- La regla trapezoidal
- La regla del punto medio
- Regla de simpson
- La integral definida
- La integral indefinida
- La altura de un rectángulo es igual a la parte inferior, menos la parte superior
- Área debajo del eje x es negativo
- Integrar en trozos
- El teorema fundamental del cálculo, toma 1
- El teorema fundamental del cálculo, toma 2
La regla trapezoidal
La regla trapezoidal le dará una aproximación bastante buena del área bajo una curva en el caso de que usted no puede - o elegir no - obtener el área exacta de la integración.
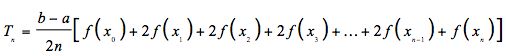
La regla del punto medio
Un área aún mejor aproximación está dada por la regla del punto medio - que utiliza rectángulos.
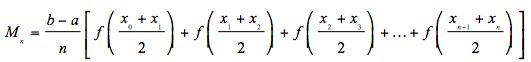
Regla de Simpson
La mejor estimación área viene dada por la regla de Simpson - que utiliza formas trapezoidales-como que tienen tapas parabólicos.
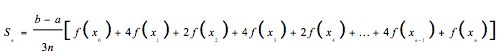
Si usted ya tiene, por ejemplo, la aproximación del punto medio durante diez rectángulos y la aproximación trapezoidal durante diez trapezoides, se puede calcular fácilmente Regla aproximación de los Simpson por diez curvas-coronado " trapezoides " con el siguiente acceso directo:
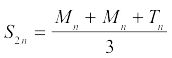
Esto le da una extraordinaria buena aproximación.
La integral definida
En esencia, lo que todas las integrales definidas,
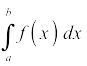
hacer es sumar un número infinito de infinitesimalmente pequeñas piezas de algo para obtener la cantidad total de la cosa entre la y b. La expresión después del símbolo integral,
(el integrando), Es siempre una expresión matemática de una pieza representativa de las cosas que está sumando.
La integral indefinida
La integral indefinida,
es la familia de todas las primitivas de
Es por eso que su respuesta tiene que terminar con " + C." Por ejemplo,
es la familia de todas las parábolas de la forma
como
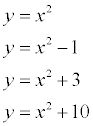
etcétera. La derivada de todas estas funciones es 2X.
La altura de un rectángulo es igual a la parte inferior, menos la parte superior
Si estás sumando rectángulos con una integral definida para obtener el área total entre dos curvas, necesita una expresión para la altura de un rectángulo representativo. Esto debería ser una obviedad: es sólo la parte superior del rectángulo y coordinar menos su parte inferior y de coordenadas.
Área debajo del eje x es negativo
Si desea, por ejemplo, el área abajo el X-eje y por encima
entre
y
la parte superior de un rectángulo representativa está en el X-eje, la función de
y su parte inferior está en
De este modo, la altura del rectángulo es
y utiliza la siguiente integral definida para obtener el área:
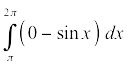
que es igual, por supuesto,
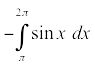
Así que esto negativo integrante le da la ordinaria positivo zona. Y es por eso que un ordinario positivo integrante le da una negativo área para las partes de una curva que están por debajo del X-eje.
Integrar en trozos
Cuando desea que el área total entre dos curvas y la " la parte superior " función cambia porque las curvas se cruzan entre sí, usted tiene que usar más de una integral definida. Cada lugar las curvas se cruzan define el borde de un área que debe integrar por separado. (Si una función cruza el X-eje, usted tiene que considerar
como la segunda función y la X intercepta como los puntos de cruce.)
El teorema fundamental del cálculo, toma 1
Dada una función de área
que barre área bajo
a saber
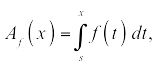
la velocidad a la que el área está siendo barrido es igual a la altura de la función original. Por lo tanto, porque la tasa es la derivada, la derivada de la función de área es igual a la función original:
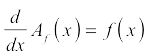
El teorema fundamental del cálculo, toma 2
Dejar F ser cualquier antiderivada de la función f- después
Cómo aproximar área con la regla de Simpson Con la regla de Simpson, que aproximar el área bajo una curva con curvas-coronado " trapezoides ". La parte superior de estas formas son secciones de parábolas. Usted puede llamar " trapezoides " porque juegan el mismo papel en la regla de Simpson…
Cómo aproximar área con la regla trapezoidal Con la regla trapezoidal, en lugar de aproximar el área mediante el uso de rectángulos (como lo hace con la izquierda, derecha, y los métodos de rectángulo del punto medio), su área aproximada con - ¿puedes adivinar? - Trapezoides.Debido a la…
Cómo hacer una aproximación área usando la notación sigma Notación Sigma es muy útil cuando se está aproximando el área bajo una curva. Por ejemplo, expresar una 8-derecha; aproximación rectángulo del área bajode 0 a 4 y calcular la aproximación.Expresa la idea básica de la suma:Esto sólo…
Cómo evaluar una integral impropia que es verticalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…
¿Cómo encontrar el valor medio de una función con el teorema del valor medio para integrales Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio es con un diagrama - echa un vistazo a continuación.El gráfico…
¿Cómo encontrar el área con la versión de acceso directo del teorema fundamental del cálculo El teorema fundamental del cálculo tiene una versión de acceso directo que hace que encontrar el área bajo una curva en un instante. Aquí está. Dejar F ser cualquier antiderivada de la función F- despuésCon esta versión del teorema…
¿Cómo encontrar zona con el método de sustitución u Puede utilizar el teorema fundamental para calcular el área debajo de una función (o simplemente para hacer cualquier edad integral definida) que se integran con el método de sustitución. Lo que quiero hacer es cambiar los límites de…
¿Cómo encontrar el área entre dos curvas Para encontrar el área entre dos curvas, lo que necesita para llegar a una expresión para un rectángulo estrecho que se encuentra en una curva y sube a otro.de X = 0 a X = 1:Para obtener la altura del rectángulo de representación en la figura,…
¿Cómo encontrar el valor medio con el teorema del valor medio para integrales Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio para integrales es con un diagrama - mira el siguiente figura.El…
¿Cómo resolver integrales impropias de funciones que tienen asíntotas verticales A resolver integrales impropias, al convertirlos en problemas de límite. No se puede hacer de ellos la manera regular. He aquí cómo resolver integrales impropias de funciones que tienen asíntotas verticales. Hay dos casos: una asíntota vertical…
Cómo dividir una integral definida en dos integrales definidas Cuando la solución de problemas de la zona, a veces es necesario dividir una integral en dos integrales definidas separadas. Aquí hay una regla simple, pero muy útil para hacer esto que parece complicado, pero es realmente muy fácil:Esta regla…
Calcular rápidamente integrales definidas utilizando el teorema fundamental Este es un teorema de integración atajo requete que utilizará para el resto de tus días naturales nacidos - o por lo menos hasta el final de su temporada con el cálculo. Este método de acceso directo es todo lo que necesita para la mayoría de…