Calcular rápidamente integrales definidas utilizando el teorema fundamental
Este es un teorema de integración atajo requete que utilizará para el resto de tus días naturales nacidos - o por lo menos hasta el final de su temporada con el cálculo. Este método de acceso directo es todo lo que necesita para la mayoría de problemas de palabras de integración.
El teorema fundamental del cálculo (segunda versión o la versión de acceso directo): Dejar F ser cualquier antiderivada de la función f- después
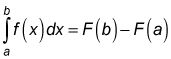
Este teorema que da el acceso directo súper para calcular una integral definida como
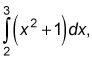
el área bajo la parábola y = X2 + 1 entre 2 y 3. Usted puede obtener esta área restando el área comprendida entre 0 y 2 de la zona comprendida entre 0 y 3, pero para hacer eso que usted necesita saber que la función de campo particular barriendo el área que comienza en cero,
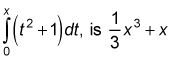
(con un C valor de cero).
La belleza del teorema de acceso directo es que usted no tiene que incluso utilizar una función de zona como
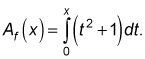
Usted acaba de encontrar cualquier antiderivada, F (X), De su función y hacer la resta, F (b) - F (la). La antiderivada más sencilla de utilizar es aquel en el que C = 0. Así que aquí es como se utiliza el teorema para encontrar el área bajo su parábola 2-3.
es una antiderivada de X2 + 1. Luego el teorema que da:
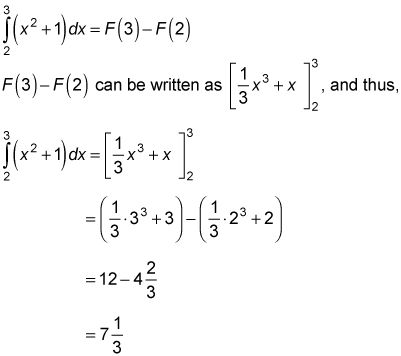
Independientemente de la función, este acceso directo que funciona, y usted no tiene que preocuparse acerca de las funciones del área. Todo lo que hacemos es F (b) - F (la).
He aquí otro ejemplo: ¿Cuál es el área bajo F (X) = eX, entre X = 3 y X 5 =? La derivada de eX es eX, así eX es una antiderivada de eX, y por lo tanto
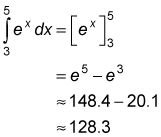
¿Qué podría ser más simple?
Áreas arriba la curva y abajo el X-eje contará como negativo áreas. Antes de continuar, es importante tocar en áreas negativas. Tenga en cuenta que con los dos ejemplos muestran aquí, la parábola, y = X2 + 1, y la función exponencial, y = eX, las áreas que estés informáticos son bajo las curvas y arriba el X-eje. Estas áreas cuentan como ordinario, positivo áreas. Pero, si una función está por debajo del X-eje, las áreas por encima de la curva y por debajo de la X-eje contará como negativo áreas.
Bien, ahora que tienes el acceso directo súper para calcular el área bajo una curva. Y si un atajo grande no fue suficiente para hacer que su día, esta tabla se enumeran algunas reglas acerca de integrales definidas que pueden hacer su vida mucho más fácil.
-
10 Cosas para recordar acerca de la integración y cálculo -
Cálculo: cómo resolver los problemas de diferenciación -
Determinar áreas firmados en un problema -
Encuentra las zonas exactas bajo una curva mediante la integral definida -
Encuentra el área bajo más de una función -
Encuentra el área entre dos funciones
¿Cómo funciona la integración: es sólo Además de lujo El significado más fundamental de la integración es sumar. Y cuando representas la integración en un gráfico, se puede ver el proceso de sumar como un resumen de finas tiras rectangulares de área para llegar al área total bajo la curva, como…
Cómo estadísticas muestra la conexión entre la diferenciación y la integración Aún tratando de entender cómo el trabajo de diferenciación e integración? No hay problema: se puede usar las estadísticas para ayudarle. Mediante el estudio de la relación entre dos gráficos simples, vas a entender la relación entre la…
Cómo aproximar área con la regla trapezoidal Con la regla trapezoidal, en lugar de aproximar el área mediante el uso de rectángulos (como lo hace con la izquierda, derecha, y los métodos de rectángulo del punto medio), su área aproximada con - ¿puedes adivinar? - Trapezoides.Debido a la…
¿Cómo encontrar el valor medio de una función con el teorema del valor medio para integrales Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio es con un diagrama - echa un vistazo a continuación.El gráfico…
¿Cómo encontrar primitivas utilizando reglas inversas Puede utilizar las reglas inversas para encontrar primitivas. Las más sencillas reglas antiderivada son los que son lo contrario de las normas derivadas que ya conoce. Estos son, primitivas automáticos de un solo paso con la excepción de la regla…
¿Cómo encontrar el área con la versión de acceso directo del teorema fundamental del cálculo El teorema fundamental del cálculo tiene una versión de acceso directo que hace que encontrar el área bajo una curva en un instante. Aquí está. Dejar F ser cualquier antiderivada de la función F- despuésCon esta versión del teorema…
¿Cómo encontrar zona con el método de sustitución u Puede utilizar el teorema fundamental para calcular el área debajo de una función (o simplemente para hacer cualquier edad integral definida) que se integran con el método de sustitución. Lo que quiero hacer es cambiar los límites de…
¿Cómo encontrar el área de una superficie de revolución Una superficie de revolución es una superficie en tres dimensiones con secciones transversales circulares, como un florero o una campana o una botella de vino. Para estos problemas, se divide la superficie en bandas circulares estrechos, calcular…
¿Cómo encontrar el área entre dos curvas Para encontrar el área entre dos curvas, lo que necesita para llegar a una expresión para un rectángulo estrecho que se encuentra en una curva y sube a otro.de X = 0 a X = 1:Para obtener la altura del rectángulo de representación en la figura,…
¿Cómo encontrar el valor medio con el teorema del valor medio para integrales Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio para integrales es con un diagrama - mira el siguiente figura.El…
Solución de problemas de integración en el cálculo Cálculo acertijo: ¿Qué teorema del valor medio, la lavadora y Métodos de Shell, y la longitud del arco y de la superficie de las fórmulas de la revolución tienen en común? Todos ellos implican la integración. La integración es además muy…
La definición de la integral definida y cómo funciona Usted puede aproximar el área bajo una curva mediante la suma de la derecha, izquierda o rectángulos punto medio. Para encontrar un área exacta, es necesario utilizar una integral definida.Al aproximar el área bajo una curva, la parte superior…