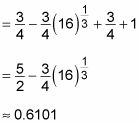Encuentra el área entre dos funciones
Para encontrar un área entre dos funciones, es necesario establecer una ecuación con una combinación de integrales definidas de ambas funciones. Por ejemplo, suponga que desea calcular el área sombreada entre y = X2 y
como se muestra en esta figura.
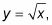
En primer lugar, observar que las dos funciones y = X2 y
intersectar donde X = 1. Esta información es importante porque le permite establecer dos integrales definidas para ayudarlo a encontrar la región A:
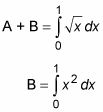
Aunque ni ecuación que da la información exacta que usted está buscando, junto te ayudan a cabo. Sólo resta la segunda ecuación de la primera como sigue:
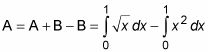
Con el problema configurado correctamente, ahora todo lo que tienes que hacer es evaluar los dos integrales:
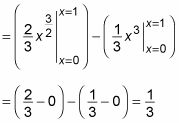
Así el área entre las dos curvas es
Como otro ejemplo, supongamos que usted desea encontrar el área entre y = X y
como se muestra en esta figura.
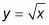
Esta vez, el área sombreada es de dos regiones separadas, etiquetada A y B. Región A está acotado superiormente por
y limitada hacia abajo por y = X. Sin embargo, para la región B, la situación se invierte, y la región está acotado superiormente por y = X y limitada hacia abajo por
Regiones C y D también están etiquetados, ya que ambos figuran en el problema.
El primer paso importante es encontrar donde se cruzan las dos funciones - es decir, donde la ecuación siguiente es cierto:
Afortunadamente, es fácil ver que X = 1 satisface esta ecuación.
Ahora usted quiere construir un par de integrales definidas para ayudarle a encontrar las áreas de la región A y la región B. Aquí hay dos que pueden ayudar con la región A:
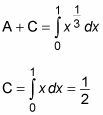
Observe que se evalúa la segunda integral definida sin cálculo, utilizando la geometría simple. Esto es perfectamente válido y un gran ahorro de tiempo.
Restando la segunda ecuación de la primera proporciona una ecuación para el área de la región A:
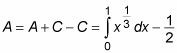
Ahora la construcción de dos integrales definidas para ayudarlo a encontrar el área de la región B:
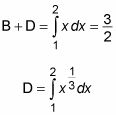
Esta vez, la primera integral definida se evalúa mediante el uso de la geometría en lugar del cálculo. Restando la segunda ecuación de la primera da una ecuación para el área de la región B:
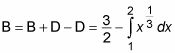
Ahora se puede establecer una ecuación para resolver el problema:
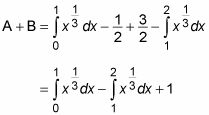
En este punto, usted está obligado a hacer un poco de cálculo:
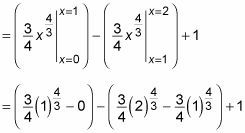
El resto es sólo aritmética:
-
La zona de los editores de la lógica pro x -
Introducir o editar ecuaciones en TI-83 Plus Equation Solver -
Escriba una ecuación en la TI-84 Plus de resolución de ecuaciones -
Resolver ecuaciones mediante la representación gráfica de su TI-84 Plus -
Cómo graficar funciones en la TI-Nspire -
Cómo trazar valores y funciones de TI-Nspire
Cómo resolver un problema de geometría Con el fin de resolver un problema de geometría, te recomiendo que leas cuidadosamente el problema, reconocer formas en el dibujo, prestar atención a las etiquetas y utilizarán todos los fórmulas que tienes que ayudarle a responder a la…
Los 4 pasos para resolver problemas La sola mención de problemas de palabras - o problemas de la historia, ya que están llamados a veces - es suficiente para enviar un escalofrío de terror en los huesos del estudiante promedio de matemáticas. En general, la solución de un…
Calcular las integrales y representando integrales como funciones Al tratar de comprender lo que hace una función integrable, primero tiene que entender dos temas relacionados: dificultades en integrales de computación y representando integrales como funciones.Integrales InformáticaPara muchas funciones de…
Determinar áreas firmados en un problema La solución a una integral definida le da la firmado área de una región. En algunos casos, el área firmado es lo que quieres, pero en algunos problemas que buscaba no firmado zona.El área firmado por encima el X-eje es positivo, pero la zona…
Determinar el área entre las curvas sin signo Usted puede utilizar el concepto de área sin firmar para medir el área entre las curvas. Por ejemplo, puede utilizar esta técnica para encontrar la zona de sombra sin firmar en la siguiente figura.Encontrar el área entre y = 4X - X2 y y = Sen X…
La evaluación de las integrales dobles Integrales dobles suelen ser integrales definidas, por lo que la evaluación de los resultados en un número real. La evaluación de las integrales dobles es similar a la evaluación de funciones anidadas: Usted trabaja de adentro hacia afuera.Puede…
Encontrar el área de una superficie de revolución Lo bueno de hallar el área de una superficie de revolución es que no hay una fórmula que puede utilizar. Memorizarlo y ya está a medio camino hecho.Para encontrar el área de una superficie de revolución entre la y b, utilizar la siguiente…
Encuentra el área bajo más de una función A veces, una sola área geométrica es descrito por más de una función. Por ejemplo, supongamos que desea encontrar el área sombreada que se muestra en la siguiente figura, el área bajo y = Sen X y y = Cos X de 0 a Pi-/ 2:La primera cosa a notar…
¿Cómo encontrar el área entre dos curvas Para encontrar el área entre dos curvas, lo que necesita para llegar a una expresión para un rectángulo estrecho que se encuentra en una curva y sube a otro.de X = 0 a X = 1:Para obtener la altura del rectángulo de representación en la figura,…
Cómo dividir una integral definida en dos integrales definidas Cuando la solución de problemas de la zona, a veces es necesario dividir una integral en dos integrales definidas separadas. Aquí hay una regla simple, pero muy útil para hacer esto que parece complicado, pero es realmente muy fácil:Esta regla…
Calcular rápidamente integrales definidas utilizando el teorema fundamental Este es un teorema de integración atajo requete que utilizará para el resto de tus días naturales nacidos - o por lo menos hasta el final de su temporada con el cálculo. Este método de acceso directo es todo lo que necesita para la mayoría de…
Cómo calcular el área de un trapecio Usted puede utilizar el derecho; truco triángulo para encontrar el área de un trapecio. La siguiente trapezoide TRAP parece un trapecio isósceles, ¿no? No se olvide - las apariencias engañan.Usted debe estar pensando, triángulos rectángulos,…