Calcular las integrales y representando integrales como funciones
Al tratar de comprender lo que hace una función integrable, primero tiene que entender dos temas relacionados: dificultades en integrales de computación
y representando integrales como funciones.Integrales Informática
Para muchas funciones de entrada, las integrales son más difíciles de calcular que los derivados. Por ejemplo, suponga que desea diferenciar e integrar la función siguiente:
y = 3X5e2X
Puede diferenciar esta función fácilmente mediante el uso de la regla del producto:
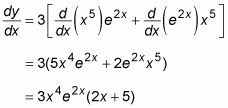
Debido a que no existe tal regla para la integración, en este ejemplo se ve obligado a buscar otro método.
La búsqueda de soluciones a las integrales puede ser negocio difícil. En comparación, la búsqueda de derivados es relativamente simple.
En representación de las integrales como funciones
Más allá de las dificultades de cálculo, de las integrales de determinadas funciones simplemente no pueden ser representados mediante el uso de las funciones a las que está acostumbrado.
Más precisamente, algunas integrales no pueden ser representados como funciones elementales - es decir, como combinaciones de las funciones que conoces de Pre-Cálculo.
Por ejemplo, tomemos la siguiente función:
Usted puede encontrar la derivada de la función fácilmente utilizando la regla de la cadena:
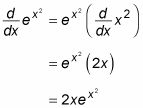
Sin embargo, la integral de la misma función,
No se puede expresar como una función - al menos, no cualquier función que usted está acostumbrado.
En su lugar, se puede expresar esta integral cualquiera exactamente - como una serie infinita - o aproximadamente - como una función que se aproxima a la integral a un nivel dado de precisión. Como alternativa, puede dejarlo como una integral, que también lo expresa muy bien para algunos propósitos.
Encuentra la integral de funciones anidadas A veces es necesario integrar una función que es la composición de dos funciones - por ejemplo, la función 2X anidada dentro de una función seno. Si estaba diferenciando, se puede utilizar la regla de la cadena. Desafortunadamente, no existe una…
Cómo antidifferentiate cualquier polinomio utilizando la suma, constante múltiple, y las reglas de alimentación Las reglas anti-diferenciación para la integración en gran medida limitar el número de integrales se puede calcular fácilmente. En muchos casos, sin embargo, puede integrar alguna polinomio en tres pasos utilizando la regla de la suma, la Regla…
Cómo evaluar una integral impropia que es verticalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…
¿Cómo integrar una función multiplicada por un conjunto de funciones anidadas A veces es necesario integrar el producto de una función (X) Y una composición de funciones (por ejemplo, la función 3X2 + 7 anidada dentro de una función de raíz cuadrada). Si estaba diferenciando, podría utilizar una combinación de la regla…
¿Cómo integrar composiciones de funciones Las composiciones de funciones - es decir, una función anidada dentro de otra - son de la forma F(g(X)). Usted puede integrarlos sustituyendo u = g(X) cuandoUsted sabe cómo integrar la función externa F.La función interna g(X) diferencia a una…
¿Cómo integrar potencias pares de senos y cosenos Puede integrar poderes incluso de senos y cosenos. Por ejemplo, si desea integrar el pecado2 X y cos2 X, que utilizaría estas identidades trigonométricas dos semi-ángulo:He aquí cómo usted integra cos2 X:Utilice la identidad-medio ángulo para…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver integrales impropias de funciones que tienen asíntotas verticales A resolver integrales impropias, al convertirlos en problemas de límite. No se puede hacer de ellos la manera regular. He aquí cómo resolver integrales impropias de funciones que tienen asíntotas verticales. Hay dos casos: una asíntota vertical…
¿Cómo resolver integrales impropias que tienen uno o dos límites infinitos de integración Una de las formas en que pueden ser integrales definidas inadecuada es cuando uno o ambos de los límites de integración son infinitas. A resolver este tipo de integral impropia al convertirlo en un problema de límite en c tiende a infinito o…
Cómo dividir una integral definida en dos integrales definidas Cuando la solución de problemas de la zona, a veces es necesario dividir una integral en dos integrales definidas separadas. Aquí hay una regla simple, pero muy útil para hacer esto que parece complicado, pero es realmente muy fácil:Esta regla…
La medición de volumen bajo una superficie usando una integral doble Una integral doble le permite medir el volumen bajo una superficie tan limitada por un rectángulo. Integrales definidas proporcionan una forma confiable de medir el área firmado entre una función y la X-eje como limitada por cualquiera de los dos…
Calcular rápidamente integrales definidas utilizando el teorema fundamental Este es un teorema de integración atajo requete que utilizará para el resto de tus días naturales nacidos - o por lo menos hasta el final de su temporada con el cálculo. Este método de acceso directo es todo lo que necesita para la mayoría de…