¿Cómo integrar composiciones de funciones
Las composiciones de funciones - es decir, una función anidada dentro de otra - son de la forma F(g(X)). Usted puede integrarlos sustituyendo u = g(X) cuando
Usted sabe cómo integrar la función externa F.
La función interna g(X) diferencia a una constante - es decir, es de la forma hacha o hacha + b.
He aquí un ejemplo. Suponga que desea integrar la función, csc2 (4X + 1).
Esta es una composición de dos funciones:
La función externa F es el csc2 (uFunción).
La función interna es g(X) = 4X + 1, que diferencia a la constante de 4.
La composición se mantiene unido por la igualdad u = 4X + 1. Es decir, las dos funciones básicas F(u) = Csc2 u y g(X) = 4X + 1 están compuestos por la igualdad u = 4X + 1 para producir la función de F(g(X)) = Csc2 (4X + 1).
Se cumplen ambos criterios, por lo que esta integral es un candidato ideal para la sustitución utilizando u = 4X + 1. Así es como se hace:
Declare una variable u y sustituir en la integral:
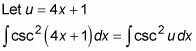
Diferenciar u = 4X + 1 y aislar la X término.
Esto le da el diferencial, du = 4dx.
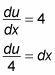
Sustituto du/ 4 para dx en la integral:
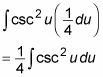
Evaluar la integral:
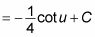
Sustituya vuelta 4X + 1 de u:
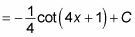
He aquí un ejemplo más. Suponga que desea evaluar la siguiente integral:
Esta es una composición de dos funciones:
La función externa F es una fracción - técnicamente, un exponente de -1 - que usted sabe cómo integrar.
La función interna es g(X) = X - 3, que diferencia a 1.
La composición se mantiene unido por la igualdad u = X - 3. Es decir, las dos funciones básicas
están compuestos por la igualdad u = X - 3 para producir la función de
Se cumplen los criterios, por lo que se puede integrar con la igualdad u = X - 3:
Declare una variable u y sustituir en la integral:
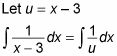
Diferenciar u = X - 3 y aislar el X término.
Esto le da el diferencial du = dx.
Sustituto du para dx en la integral:
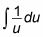
Evaluar la integral:
= Ln |u| + C
Sustituya la espalda X - 3 para u:
= Ln |X - 3 | + C
-
Cálculo II para dummies -
Calcular las integrales y representando integrales como funciones -
La evaluación de las integrales dobles -
Encontrar la integral de un producto de dos funciones -
Encuentra la integral de funciones anidadas -
Cómo antidifferentiate cualquier polinomio utilizando la suma, constante múltiple, y las reglas de alimentación
Cómo evaluar una integral impropia que es verticalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…
¿Cómo integrar una serie de potencias Debido a la serie de potencia se asemejan polinomios, son fáciles de integrar el uso de un proceso de tres pasos simples que utiliza la regla de la suma, la Regla múltiplo constante, y la Regla de energía.Por ejemplo, echar un vistazo a la…
¿Cómo integrar una función multiplicada por un conjunto de funciones anidadas A veces es necesario integrar el producto de una función (X) Y una composición de funciones (por ejemplo, la función 3X2 + 7 anidada dentro de una función de raíz cuadrada). Si estaba diferenciando, podría utilizar una combinación de la regla…
¿Cómo integrar potencias pares de senos y cosenos Puede integrar poderes incluso de senos y cosenos. Por ejemplo, si desea integrar el pecado2 X y cos2 X, que utilizaría estas identidades trigonométricas dos semi-ángulo:He aquí cómo usted integra cos2 X:Utilice la identidad-medio ángulo para…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
Cómo utilizar identidades para integrar las funciones trigonométricas Usted se sorprenderá de lo mucho que avanzar a menudo se puede hacer cuando se integra una función de trigonometría desconocida por primera ajustar usando las identidades Básica Cinco trig:El poder invisible de estas identidades se encuentra en…
Cómo utilizar la integración por partes Al hacer Cálculo, la fórmula de integración por partes te da la opción de romper el producto de dos funciones a sus factores e integrarlo en una forma alterada. Para utilizar la integración por partes en cálculo, siga estos pasos:Descomponer…
Integrar una función utilizando el caso secante Cuando la función que se está integrando incluye un término de la forma (bx2 - la2)n, llamar su triángulo sustitución trigonométrica para el caso secante. Por ejemplo, suponga que desea evaluar esta integral:Este es un caso secante, debido a…
Integrar una función utilizando el caso sine Cuando la función está integrando incluye un término de la forma (la2 - bx2)n, llamar su triángulo sustitución trigonométrica para el caso sinusoidal. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso sinusoidal,…
Integrar una función utilizando el caso tangente Cuando la función está integrando incluye un término de la forma (la2 + X2)n, llamar su trigonometría triángulo de sustitución para el caso tangente. Por ejemplo, supongamos que desea evaluar la siguiente integral:Este es un caso tangente,…
Saber cuándo integrar por partes Es importante reconocer que la integración por partes es útil. Para empezar, aquí hay dos casos importantes cuando la integración por partes es definitivamente el camino a seguir:La función logarítmica ln XLas cuatro primeras funciones…
Resolver funciones compuestos donde la función interna es hacha Al calcular problemas de Cálculo, algunas integrales de funciones compuestos F (g(X)) Son fáciles de hacer rápidamente. Estos incluyen funciones compuestos para los que saben cómo integrar la función externa F, y la función interna g(X) Es de…