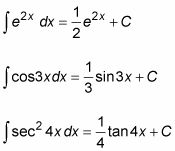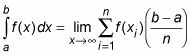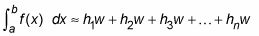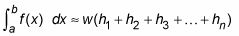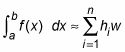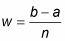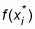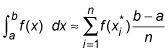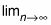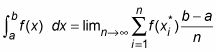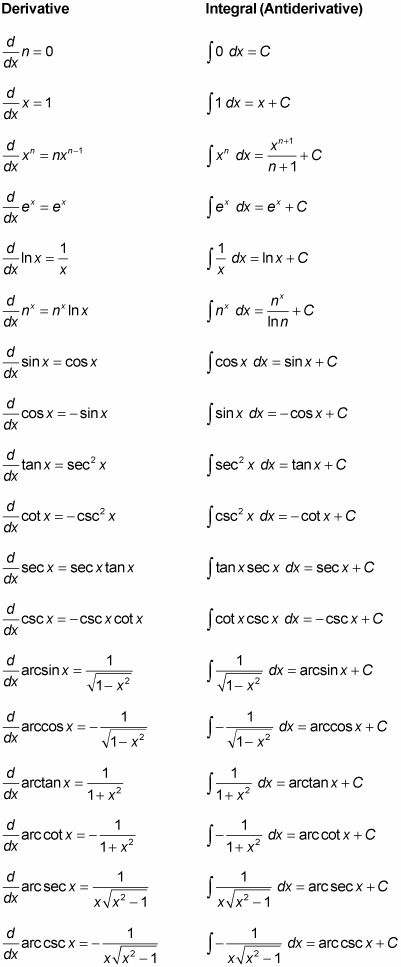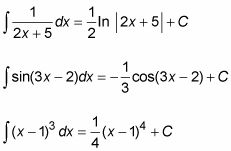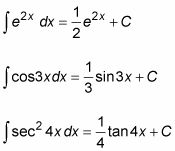La siguiente tabla muestra cómo diferenciar e integrar 18 de las funciones más comunes. Como puede ver, la integración invierte diferenciación, devolviendo la función a su estado original, hasta una constante C
.
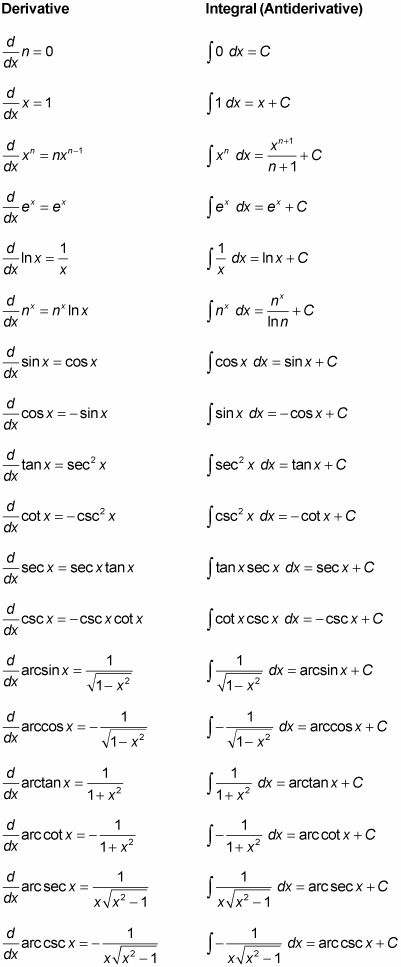
La fórmula de Riemann Sum Para la integral definida
La fórmula de Riemann Sum proporciona una definición precisa de la integral definida como el límite de una serie infinita. La fórmula de Riemann Sum es el siguiente:
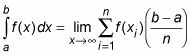
A continuación se presentan los pasos para aproximar una integral usando seis rectángulos:
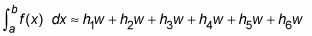
Aumentar el número de rectángulos (n) Para crear una mejor aproximación:
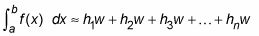
Simplifique esta fórmula por factorizar w de cada término:
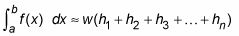
Utilice el símbolo de sumatoria para hacer esta fórmula aún más compacto:
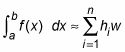
El valor w es el ancho de cada rectángulo:
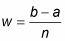
Cada h valor es el altura de un rectángulo diferente:
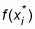
Así que aquí está la fórmula de Riemann Sum para aproximación una integral usando n rectángulos:
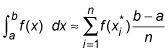
Para una mejor aproximación, utilizar el límite
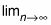
para permitir que el número de rectángulos de acercarse infinito:
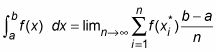
Integración por partes con el Método-DI agonal
El método-DI agonal es básicamente la integración por partes con un gráfico que ayuda a organizar la información. Este método es especialmente útil cuando se necesita para integrar por partes más de una vez para resolver un problema. Utilice la siguiente tabla para la integración por partes utilizando el método-DI agonal:
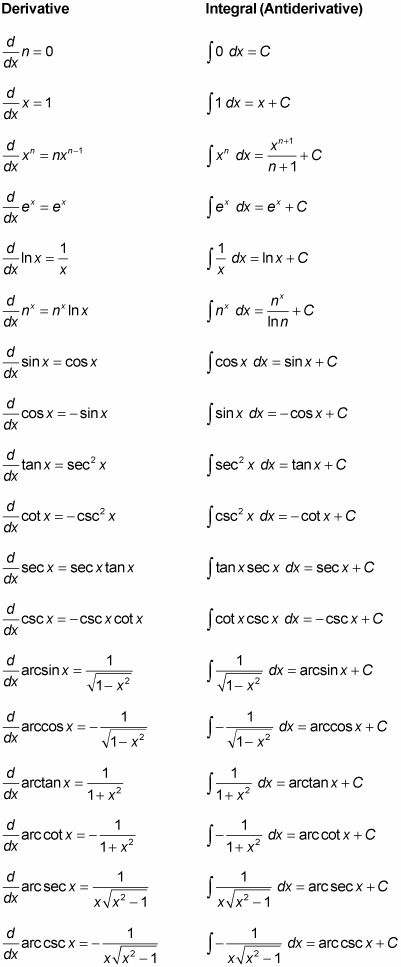
La regla de la suma, la Regla múltiplo constante, y el estado de alimentación de Integración
Al realizar la integración, hay tres reglas importantes que usted necesita saber: la regla de la suma, la regla múltiplo constante, y la regla de la potencia.
La regla de la suma para la Integración te dice que está bien para integrar a largo plazo expresiones a término. Sentimos formalmente:
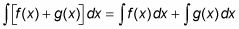
La Regla múltiplo constante de Integración te dice que está bien para pasar una constante fuera de una integral antes de integrar. Aquí se expresa en símbolos:
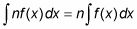
La regla de la potencia de Integración permite integrar cualquier poder real de X (excepto -1). Aquí está la regla de la potencia expresado formalmente:
dónde n # 8800- -1
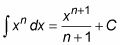
Cómo resolver Integrales con Sustitución de variables
En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.
Declare una variable u, configurarlo igual a una expresión algebraica que aparece en la integral, y luego sustituir u para esta expresión en la integral.
Diferenciar u encontrar
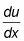
y luego aislar todo X variables en un lado del signo igual.
Hacer otra sustitución de cambiar dx y todas las demás ocurrencias de X en la integral de una expresión que incluye du.
Integrar mediante el uso de u como su nueva variable de integración.
Exprese su respuesta en términos de X.
Cómo utilizar Integración por partes
Al hacer Cálculo, la fórmula de integración por partes te da la opción de romper el producto de dos funciones a sus factores e integrarlo en una forma alterada. Para utilizar la integración por partes en cálculo, siga estos pasos:
Descomponer toda la integral (incluyendo dx) En dos factores.
Deja que el factor sin dx igual u y el factor con dx igual dv.
Diferenciar u encontrar du, e integrar dv encontrar v.
Utilice la fórmula:
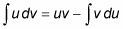
Evaluar el lado derecho de esta ecuación para resolver la integral.
Cómo solucionar Funciones compuestas donde la función interna es hacha + b
Algunas integrales de funciones compuestos F (g(X)) Son fáciles de hacer rápidamente en Cálculo. Estos incluyen funciones compuestos para los que saben cómo integrar la función externa F, y la función interna g(X) Es de la forma hacha + b - es decir, que diferencia a una constante.
Aquí hay unos ejemplos:
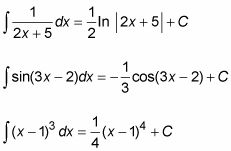
Resolver Funciones compuestas donde la función interna es hacha
Al calcular problemas de Cálculo, algunas integrales de funciones compuestos F (g(X)) Son fáciles de hacer rápidamente. Estos incluyen funciones compuestos para los que saben cómo integrar la función externa F, y la función interna g(X) Es de la forma hacha - es decir, que diferencia a una constante.
Aquí hay unos ejemplos: