Cómo utilizar la integración por partes
Al hacer Cálculo, la fórmula de integración por partes te da la opción de romper el producto de dos funciones a sus factores e integrarlo en una forma alterada. Para utilizar la integración por partes en cálculo, siga estos pasos:
Descomponer toda la integral (incluyendo dx) En dos factores.
Deja que el factor sin dx igual u y el factor con dx igual dv.
Diferenciar u encontrar du, e integrar dv encontrar v.
Utilice la fórmula:
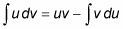
Evaluar el lado derecho de esta ecuación para resolver la integral.
Encuentra la integral de funciones anidadas A veces es necesario integrar una función que es la composición de dos funciones - por ejemplo, la función 2X anidada dentro de una función seno. Si estaba diferenciando, se puede utilizar la regla de la cadena. Desafortunadamente, no existe una…
¿Cómo se hace la integración por partes Integrando por partes es la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que no puede hacerlo en un producto simple, menos un integrante que…
Cómo hacer una integración sencilla de las piezas Integrando por partes es la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que no puede hacerlo en un producto simple, menos un integrante que…
Cómo evaluar una integral impropia que es horizontalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA horizontalmente infinita integral impropia contiene ya sea # 8734- o - # 8734- (o ambos) como un límite de la integración.Evaluación de una integral impropia es un…
¿Cómo integrar una función multiplicada por un conjunto de funciones anidadas A veces es necesario integrar el producto de una función (X) Y una composición de funciones (por ejemplo, la función 3X2 + 7 anidada dentro de una función de raíz cuadrada). Si estaba diferenciando, podría utilizar una combinación de la regla…
¿Cómo resolver (y el factor) una ecuación cuadrática con la fórmula cuadrática Una ecuación cuadrática es cualquier segundo grado ecuación polinómica - que es cuando la mayor potencia de X, o cualquier otra variable se usa, es de 2. La solución o soluciones de una ecuación de segundo grado,Resolver la ecuación,con la…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver integrales mediante la integración por partes Usted puede pensar en la integración por partes como la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que poder't hacerlo en un producto…
La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede…
Integración por problemas partes donde usted va en círculos A veces, si se utiliza la integración por partes dos veces, a volver al punto de partida de - que, a diferencia de perderse, no es una pérdida de tiempo.En primer lugar, utilice el LIATE recurso mnemotécnico para recoger su u:Para recoger tu u,…
Saber cuándo integrar por partes Es importante reconocer que la integración por partes es útil. Para empezar, aquí hay dos casos importantes cuando la integración por partes es definitivamente el camino a seguir:La función logarítmica ln XLas cuatro primeras funciones…
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…