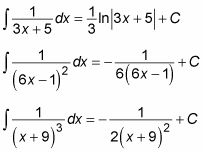La creación de fracciones parciales cuando se tiene factores lineales distintos
Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador es el producto de distinto factores lineales - es decir, los factores que son lineales no repetitivo.
Por ejemplo, puede cambiar esto:
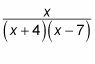
a esto:
Tenga en cuenta que para cada factor lineal distinta en el denominador, es necesario agregar una fracción parcial de la siguiente forma:
Por ejemplo, suponga que desea integrar la siguiente expresión racional:
El denominador es el producto de tres factores lineales distintos - X, (X + 2), y (X - 5) - por lo que es igual a la suma de tres fracciones con estos factores como denominadores:
El número de factores lineales distintos en el denominador de la expresión original determina el número de fracciones parciales. En este ejemplo, la presencia de tres factores en el denominador de la expresión original produce tres fracciones parciales.
Tienes dos maneras de encontrar las incógnitas en una suma de fracciones parciales. La manera fácil y rápida es mediante el uso de las raíces de los polinomios. Desafortunadamente, este método no siempre encontrar todas las incógnitas en un problema, a pesar de que a menudo se encuentra a algunos de ellos. La segunda forma es la creación de un sistema de ecuaciones.
Cuando una suma de fracciones parciales tiene factores lineales distintos, puede utilizar las raíces de estos factores lineales para encontrar los valores de incógnitas:
Para encontrar los valores de las incógnitas LA, B, y C, primero obtener un denominador común en el lado derecho de esta ecuación (el mismo denominador que está en el lado izquierdo):
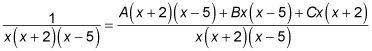
Ahora multiplique ambos lados por este denominador:
1 = LA(X + 2) (X - 5) + Bx(X - 5) + Cx(X + 2)
Para encontrar los valores de LA, B, y C, sustituir las raíces de los tres factores (0, -2, y 5):
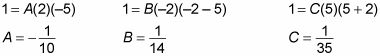
Al conectar estos valores en la ecuación original que da:
Esta expresión es equivalente a lo que usted comenzó con, pero es mucho más fácil de integrar. Para hacerlo, utilice la regla de la suma para dividirla en tres integrales, la regla múltiplo constante para mover coeficientes fraccionarios fuera cada sustitución integral y variable para hacer la integración. Aquí está la respuesta para que pueda probarlo:
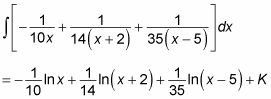
Esta respuesta utiliza K Más bien que C para representar la constante de integración para evitar la confusión, debido a que ya usaste C en las fracciones parciales anteriores.
Cuando usted comienza con un factor lineal distinta, usando fracciones parciales te deja con una integral de la forma siguiente:
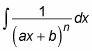
Integrar con la sustitución de variables u = hacha + b así que eso du = a dx y
Esta sustitución da como resultado la siguiente integral:
Aquí están algunos ejemplos:
Cómo reducir una fracción a su mínima expresión Incluso si se ven diferentes fracciones, que en realidad puede representar la misma cantidad- en otras palabras, una de las fracciones habrá reducido términos en comparación con el otro. Puede que tenga que reducir los términos de las fracciones…
Cómo restar fracciones con el mismo denominador Restar fracciones con el mismo denominador (número inferior) es fácil. Cuando los denominadores son los mismos, sólo puede pensar en las fracciones como pedazos de torta.Para restar una fracción de otro cuando ambos tienen el mismo denominador,…
Cómo descomponer fracciones parciales Un proceso llamado fracciones parciales toma un fracción y la expresa como la suma o diferencia de otras dos fracciones. En cálculo, este proceso es útil antes de integrar una función. Debido a que la integración es mucho más fácil cuando el…
Descomponer fracciones parciales en 8 pasos Cuando su instructor de pre-cálculo le pide que para descomponer fracciones parciales, que en realidad no es tan complicado como parece. El proceso de descomponer una fracción parcial requiere para separar la fracción en dos fracciones (o a veces…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales Usted puede utilizar el método de fracciones parciales para integrar funciones racionales (Recordemos que una función racional es uno polinomio dividido por otro.) La idea básica detrás del enfoque de fracciones parciales es " unadding " una…
La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede…
Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles A veces no se puede factorizar un denominador todo el camino a factores lineales porque algunas ecuaciones cuadráticas son irreductibles - al igual que los números primos, no pueden tenerse en cuenta.Comprobar el discriminante. Puede comprobar…
La creación de fracciones parciales cuando se ha repetido factores lineales Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores lineales…
La creación de fracciones parciales cuando se ha repetido factores cuadráticos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores cuadráticos…
La creación de fracciones parciales cuando tiene distintos factores Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es cuando el denominador es el…
Preparación ASVAB: cómo sumar y restar fracciones Adición y sustracción de fracciones para el ASVAB (o para cualquier otro propósito) puede ser tan simple como multiplicar y dividir, o puede ser más difícil. A medida que la siguiente información muestra, todo depende de si las fracciones…