Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles
A veces no se puede factorizar un denominador todo el camino a factores lineales porque algunas ecuaciones cuadráticas son irreductibles - al igual que los números primos, no pueden tenerse en cuenta.
Comprobar el discriminante. Puede comprobar fácilmente si un cuadrática (hacha2 + bx + c) Es reducible o no mediante la comprobación de su discriminante, b2 - 4ac. Si el discriminante es negativo, el cuadrática es irreducible. Si el discriminante es un cuadrado perfecto como 0, 1, 4, 9, 16, 25, etc., el cuadrática puede tenerse en cuenta factores como la que estamos acostumbrados a ver como (2X - 5) (X + 5). La última posibilidad es que el discriminante es igual a un número positivo no cuadrado, como con el cuadrática X2 + 10X + 1, por ejemplo, que tiene un discriminante de 96. En ese caso, la cuadrática se puede factorizar, pero usted consigue factores feas que implican raíces cuadradas. Afortunadamente, estos problemas son poco comunes.
Utilizando la técnica de fracciones parciales con cuadráticas irreductibles es un poco diferente. Aquí hay un problema: Integre
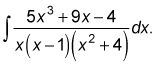
Factorizar el denominador.
¡Ya está hecho! Tenga en cuenta que X2 + 4 es irreductible porque su discriminante es negativo.
Romper la fracción en una suma de "fracciones parciales."
Si usted tiene un factor cuadrático irreducible (como el X2 + 4), el numerador de la fracción parcial necesita dos incógnitas capital de letras en lugar de sólo uno. Usted los escribe en forma de Px + Q.
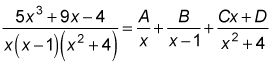
Multiplicar ambos lados de esta ecuación por la izquierda; denominador lado.
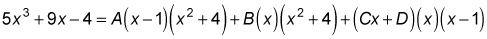
Tome las raíces de los factores lineales y conectarlos - uno a la vez - en X en la ecuación de la Etapa 3, y luego resolver.
Si X = 0, Si X = 1,
-4 = -4LA10 = 5B
LA = 1B = 2
Usted no puede resolver todas las incógnitas por taponamiento en las raíces de los factores lineales, por lo que tiene más trabajo que hacer.
Enchufe en la ecuación Paso 3 los valores conocidos de LA y B y cualquiera de los dos valores para X no se utiliza en el paso 4 (números bajos hacen que la aritmética más fácil) para obtener un sistema de dos ecuaciones en C y D.
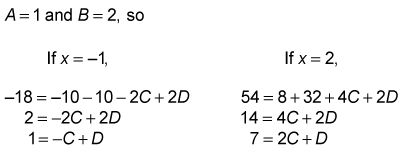
Resuelve el sistema: 1 = -C + D y 7 = 2C + D.
Usted debe obtener C = 2 y D = 3.
Dividir la integral original y de integrar.
Utilizando los valores obtenidos en los pasos 4 y 6, LA = 1, B = 2, C = 2, y D = 3, y la ecuación de la Etapa 2, se puede dividir la integral original en tres piezas:
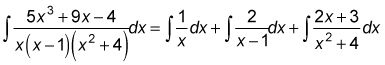
Y con álgebra simple, se puede dividir el tercer integrante de la derecha en dos partes, lo que resulta en la fracción final descomposición parcial:
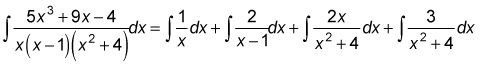
Los dos primeros integrales son fáciles. Para el tercero, se utiliza la sustitución con
El cuarto se hace con la regla de arco tangente, que debe memorizar:
Cómo descomponer fracciones parciales Un proceso llamado fracciones parciales toma un fracción y la expresa como la suma o diferencia de otras dos fracciones. En cálculo, este proceso es útil antes de integrar una función. Debido a que la integración es mucho más fácil cuando el…
Descomponer fracciones parciales en 8 pasos Cuando su instructor de pre-cálculo le pide que para descomponer fracciones parciales, que en realidad no es tan complicado como parece. El proceso de descomponer una fracción parcial requiere para separar la fracción en dos fracciones (o a veces…
¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales Usted puede utilizar el método de fracciones parciales para integrar funciones racionales (Recordemos que una función racional es uno polinomio dividido por otro.) La idea básica detrás del enfoque de fracciones parciales es " unadding " una…
¿Cómo resolver (y el factor) una ecuación cuadrática con la fórmula cuadrática Una ecuación cuadrática es cualquier segundo grado ecuación polinómica - que es cuando la mayor potencia de X, o cualquier otra variable se usa, es de 2. La solución o soluciones de una ecuación de segundo grado,Resolver la ecuación,con la…
¿Cómo resolver una ecuación cuadrática cuando no lo hará factor de Cuando se le preguntó a resolver una ecuación cuadrática que usted apenas no puede parecerse al factor (o que simplemente no hace de los factores), hay que emplear otras formas de resolver la ecuación, como mediante el uso de la fórmula…
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…
La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede…
La creación de fracciones parciales cuando se ha repetido factores lineales Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores lineales…
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…
La creación de fracciones parciales cuando se ha repetido factores cuadráticos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores cuadráticos…
La creación de fracciones parciales cuando tiene distintos factores Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es cuando el denominador es el…
Cómo factorizar expresiones trigonométricas con títulos superiores a 2 Aunque factoring cuadráticas es una brisa, factoring ecuaciones de trigonometría con grados más altos pueden ser un poco desagradable si usted no tiene una situación agradable, como sólo dos términos o una ecuación de segundo grado similar. A…