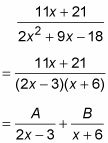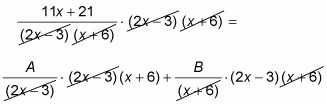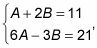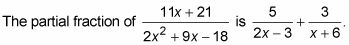Cómo descomponer fracciones parciales
Un proceso llamado fracciones parciales toma un fracción y la expresa como la suma o diferencia de otras dos fracciones. En cálculo, este proceso es útil antes de integrar una función. Debido a que la integración es mucho más fácil cuando el grado de una función racional es 1 en el denominador, la fracción de la descomposición parcial es una herramienta útil para usted.
El proceso de descomposición de fracciones parciales requiere para separar la fracción en dos fracciones (o a veces más) inconexas con las variables (por lo general LA, B, C, y así sucesivamente) de pie en como marcadores de posición en el numerador. A continuación, puede establecer un sistema de ecuaciones para resolver estas variables. Por ejemplo, debe seguir estos pasos para escribir la descomposición en fracciones parciales de
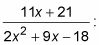
Factorizar el denominador y reescribir como LA más de un factor y B sobre el otro.
Esto se hace porque quiere romper la fracción en dos. El proceso se desarrolla de la siguiente manera:
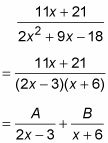
Multiplica cada término que has creado por el denominador factorizada y luego cancela.
Usted multiplica un total de tres veces en este ejemplo:
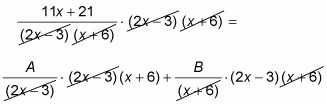
Esto equivale a 11X + 21 = LA(X + 6) + B(2X - 3).
Distribuir LA y B.
Esto le da 11X + 21 = Hacha + 6LA + 2Bx - 3B.
En el lado derecho de la ecuación única, ponga todos los términos con un X juntos y todos los términos sin juntos.
Reorganizar le da 11X + 21 = Hacha + 2Bx + 6LA - 3B.
Factorizar el X a partir de los términos en el lado derecho.
Ahora tiene 11X + 21 = (LA + 2B)X + 6LA - 3B.
Crear un sistema de esta ecuación haciendo pares términos.
Para una ecuación para trabajar, todo debe estar en equilibrio. Debido a este hecho, los coeficientes de X deben ser iguales y las constantes deben ser iguales. Si el coeficiente de X es 11 a la izquierda y LA + 2B a la derecha, se puede decir que 11 = LA + 2B es una ecuación. Las constantes son los términos con ninguna variable, y en este caso, la constante de la izquierda es 21. En el lado derecho, 6LA - 3B es la constante (porque no hay ninguna variable adjunta) y así 21 = 6LA - 3B.
Resuelve el sistema, utilizando la sustitución o eliminación.
En este ejemplo, se utiliza la eliminación de este sistema. Si
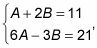
se puede multiplicar la ecuación por encima -6 y luego añadir eliminar y resolver. Usted encontrará que LA = 5 y B = 3.
Escribe la solución como la suma de dos fracciones.
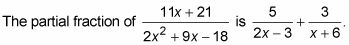
Sobre el autor
 Cómo restar fracciones con el mismo denominador
Cómo restar fracciones con el mismo denominador Restar fracciones con el mismo denominador (número inferior) es fácil. Cuando los denominadores son los mismos, sólo puede pensar en las fracciones como pedazos de torta.Para restar una fracción de otro cuando ambos tienen el mismo denominador,…
 En fracciones, uno es el número más fácil
En fracciones, uno es el número más fácil Con fracciones, la relación entre los números, no los números reales en sí, es más importante. Comprender cómo multiplicar y dividir fracciones pueden darle una comprensión más profunda de por qué se puede aumentar o disminuir los números…
 Descomponer fracciones parciales en 8 pasos
Descomponer fracciones parciales en 8 pasos Cuando su instructor de pre-cálculo le pide que para descomponer fracciones parciales, que en realidad no es tan complicado como parece. El proceso de descomponer una fracción parcial requiere para separar la fracción en dos fracciones (o a veces…
 ¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales
¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales Usted puede utilizar el método de fracciones parciales para integrar funciones racionales (Recordemos que una función racional es uno polinomio dividido por otro.) La idea básica detrás del enfoque de fracciones parciales es " unadding " una…
 La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas
La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede…
 Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles
Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles A veces no se puede factorizar un denominador todo el camino a factores lineales porque algunas ecuaciones cuadráticas son irreductibles - al igual que los números primos, no pueden tenerse en cuenta.Comprobar el discriminante. Puede comprobar…
 La creación de fracciones parciales cuando se ha repetido factores lineales
La creación de fracciones parciales cuando se ha repetido factores lineales Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores lineales…
 La creación de fracciones parciales cuando se tiene factores lineales distintos
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…
 La creación de fracciones parciales cuando se ha repetido factores cuadráticos
La creación de fracciones parciales cuando se ha repetido factores cuadráticos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores cuadráticos…
 La creación de fracciones parciales cuando tiene distintos factores
La creación de fracciones parciales cuando tiene distintos factores Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es cuando el denominador es el…
 Sistemas de ecuaciones utilizadas en pre-cálculo
Sistemas de ecuaciones utilizadas en pre-cálculo LA sistema de ecuaciones es una colección de dos o más ecuaciones que implican dos o más variables. Si el número de ecuaciones es igual al número de variables diferentes, entonces usted puede ser capaz de encontrar una solución única que es…
 Romper o combinar fracciones para resolver una identidad trigonometría
Romper o combinar fracciones para resolver una identidad trigonometría Una identidad trigonométrica con fracciones puede trabajar a su ventaja- te dan una plan de ataque. Usted puede trabajar hacia la eliminación de la fracción y, en el proceso, resolver el problema. Dos de las principales técnicas para trabajar…