La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas
Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede dividirse en factores lineales).
Si el discriminante es negativo, el cuadrática es irreducible.
Usted puede utilizar la técnica de fracciones parciales para funciones cuyos denominadores pueden tenerse en cuenta a factores lineales. Sin embargo, el uso de esta técnica es un poco diferente cuando hay factores cuadráticos irreducibles.
Factorizar el denominador.
¡Ya está hecho!
Romper la fracción en una suma de " fracciones parciales ".
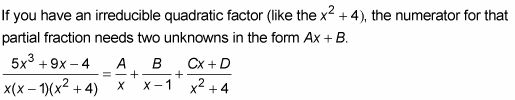
Multiplicar ambos lados de esta ecuación por la izquierda; denominador lado.
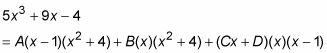
Tome las raíces de los factores lineales y conectarlos - uno a la vez - en X en la ecuación de la Etapa 3, y luego resolver.
Si X = 0
-4 = -4LA
LA = 1
Si X = 1
10 = 5B
B = 2
Enchufe en la ecuación Paso 3 los valores conocidos de LA y B y cualquiera de los dos valores para X no se utiliza en el paso 4 (números bajos hacen que la aritmética más fácil) para obtener un sistema de dos ecuaciones en C y D.
LA = 1 y B = 2, por lo
Si X = -1
-18 = -10 - 10 - 2C + 2D
2 = -2C + 2D
1 = -C + D
Si X = 2
54 = 8 + 32 + 4C + 2D
14 = 4C + 2D
7 = 2C + D
Resuelve el sistema: 1 = -C + D y 7 = 2C + D.
Usted debe obtener C = 2 y D = 3.
Dividir la integral original y de integrar.
Utilizando los valores obtenidos en los pasos 4 y 6, LA = 1, B = 2, C = 2, y D = 3, y la ecuación de la Etapa 2, se puede dividir la integral original en tres piezas:
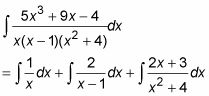
Y con álgebra básica, se puede dividir el tercer integrante de arriba en dos partes, lo que resulta en la fracción final descomposición parcial:
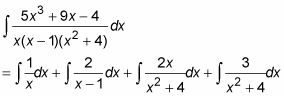
Los dos primeros integrales son fáciles, de un solo paso integrales de registro natural.
Después de la sustitución, ésta se convierte en otro logaritmo natural integral.
El cuarto se hace con la regla arco tangente.
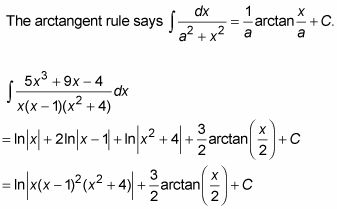
Usted no puede resolver todas las incógnitas por taponamiento en las raíces de los factores lineales, por lo que tiene más trabajo que hacer.
¿Te acuerdas de las reglas de registro, ¿verdad? El paso final utiliza el registro de una regla de producto a combinar los tres registros en una sola.
Cómo descomponer fracciones parciales Un proceso llamado fracciones parciales toma un fracción y la expresa como la suma o diferencia de otras dos fracciones. En cálculo, este proceso es útil antes de integrar una función. Debido a que la integración es mucho más fácil cuando el…
Descomponer fracciones parciales en 8 pasos Cuando su instructor de pre-cálculo le pide que para descomponer fracciones parciales, que en realidad no es tan complicado como parece. El proceso de descomponer una fracción parcial requiere para separar la fracción en dos fracciones (o a veces…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales Usted puede utilizar el método de fracciones parciales para integrar funciones racionales (Recordemos que una función racional es uno polinomio dividido por otro.) La idea básica detrás del enfoque de fracciones parciales es " unadding " una…
¿Cómo resolver (y el factor) una ecuación cuadrática con la fórmula cuadrática Una ecuación cuadrática es cualquier segundo grado ecuación polinómica - que es cuando la mayor potencia de X, o cualquier otra variable se usa, es de 2. La solución o soluciones de una ecuación de segundo grado,Resolver la ecuación,con la…
Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles A veces no se puede factorizar un denominador todo el camino a factores lineales porque algunas ecuaciones cuadráticas son irreductibles - al igual que los números primos, no pueden tenerse en cuenta.Comprobar el discriminante. Puede comprobar…
La creación de fracciones parciales cuando se ha repetido factores lineales Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores lineales…
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…
La creación de fracciones parciales cuando se ha repetido factores cuadráticos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores cuadráticos…
La creación de fracciones parciales cuando tiene distintos factores Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es cuando el denominador es el…
¿Cómo trabajar ambos lados de una identidad trig Con una identidad trigonometría, trabajando en ambos lados de la ecuación es aún más divertido que trabajar en ambos lados de una algebraico ecuación. En álgebra, puede multiplicar cada lado por el mismo número, cuadrado ambos lados, añadir…
Preparación ASVAB: cómo sumar y restar fracciones Adición y sustracción de fracciones para el ASVAB (o para cualquier otro propósito) puede ser tan simple como multiplicar y dividir, o puede ser más difícil. A medida que la siguiente información muestra, todo depende de si las fracciones…