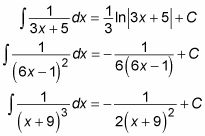La creación de fracciones parciales cuando se ha repetido factores lineales
Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores lineales repetidos. Estos son difíciles de trabajar porque cada factor requiere más de una fracción parcial.
Para cada factor lineal al cuadrado en el denominador, agregue de dos fracciones parciales en la forma siguiente:
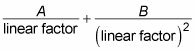
Para cada factor cuadrático en el denominador que está elevado a la tercera potencia, añadir de tres fracciones parciales en la forma siguiente:
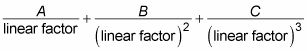
En términos generales, cuando un factor lineal se eleva a la nésima potencia, añadir n fracciones parciales. Por ejemplo, suponga que desea integrar la siguiente expresión:
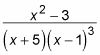
Esta expresión contiene todos los factores lineales, pero uno de estos factores (X + 5) es no repetido y la otra (X - 1) se eleva a la tercera potencia. Configure sus fracciones parciales de esta manera:
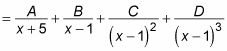
Qué producirá:
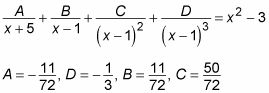
Como puede ver, este ejemplo añade una fracción parcial para tener en cuenta el factor de no repetitivo y tres para tener en cuenta el factor de repetición.
Cuando usted comienza con un factor lineal, usando fracciones parciales te deja con una integral de la forma siguiente:
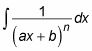
Integrar todos estos casos mediante la sustitución de variables u = hacha + b así que eso du = a dx y
Esta sustitución da como resultado la siguiente integral:
Aquí están algunos ejemplos:
Cómo restar fracciones con diferentes denominadores Cuando quiera restar fracciones con diferentes denominadores, usted tiene una opción de métodos: el camino más fácil, el truco rápido, y la manera tradicional.La manera fácil siempre funciona, y usted debe utilizar este método para la mayor…
Cómo restar fracciones con denominadores comunes Como con la adición, restando fracciones que tienen el mismo denominador (también llamado común denominador) Es muy simple: sólo resta el segundo numerador de la primera y mantener el denominador de la misma. En algunos casos, es posible que…
En fracciones, uno es el número más fácil Con fracciones, la relación entre los números, no los números reales en sí, es más importante. Comprender cómo multiplicar y dividir fracciones pueden darle una comprensión más profunda de por qué se puede aumentar o disminuir los números…
Cómo descomponer fracciones parciales Un proceso llamado fracciones parciales toma un fracción y la expresa como la suma o diferencia de otras dos fracciones. En cálculo, este proceso es útil antes de integrar una función. Debido a que la integración es mucho más fácil cuando el…
Descomponer fracciones parciales en 8 pasos Cuando su instructor de pre-cálculo le pide que para descomponer fracciones parciales, que en realidad no es tan complicado como parece. El proceso de descomponer una fracción parcial requiere para separar la fracción en dos fracciones (o a veces…
¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales Usted puede utilizar el método de fracciones parciales para integrar funciones racionales (Recordemos que una función racional es uno polinomio dividido por otro.) La idea básica detrás del enfoque de fracciones parciales es " unadding " una…
La identificación, y ecuaciones diferenciales parciales lineales ordinarias Ecuaciones diferenciales (DES) vienen en muchas variedades. Y diferentes variedades de ED se pueden resolver utilizando diferentes métodos. Puede clasificar DES como Des ordinaria y parcial. Además de esta distinción se pueden distinguir…
La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede…
Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles A veces no se puede factorizar un denominador todo el camino a factores lineales porque algunas ecuaciones cuadráticas son irreductibles - al igual que los números primos, no pueden tenerse en cuenta.Comprobar el discriminante. Puede comprobar…
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…
La creación de fracciones parciales cuando se ha repetido factores cuadráticos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores cuadráticos…
La creación de fracciones parciales cuando tiene distintos factores Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es cuando el denominador es el…