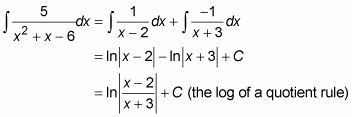¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales
Usted puede utilizar el método de fracciones parciales para integrar funciones racionales (Recordemos que una función racional es uno polinomio dividido por otro.) La idea básica detrás del enfoque de fracciones parciales es " unadding " una fracción:
Antes de utilizar la técnica de fracciones parciales, usted tiene que comprobar que su integrando es una " adecuado " fracción - que es uno donde el grado del numerador es menor que el grado del denominador. Si el integrando es " inadecuado, " como
que tienes que hacer primero la división larga polinómica para transformar la fracción impropia en una suma de un polinomio (que a veces se acaba de haber un número) y una fracción propia. Aquí está la división de esta fracción impropia (sin explicación). Básicamente, funciona igual que la división de tiempo regular.
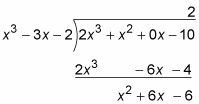
Con la división regular, si se divide en 23 4, se obtiene un cociente de 5 y un resto de 3, que le dice que
El resultado de la división polinómica anterior le dice lo mismo.
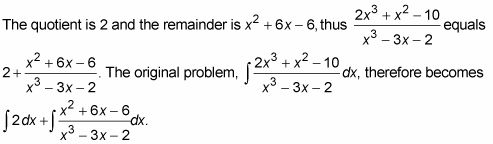
La primera integral es sólo 2X. A continuación, hacer la segunda integral con el método de fracciones parciales.
Así es como funciona el método, pero vamos a una entrada integrante menos complicado que el inmediatamente anteriormente que esto hará que la técnica más fácil de seguir.
Factorizar el denominador.
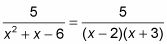
Romper la fracción a la derecha en una suma de fracciones, donde cada factor del denominador en el paso 1 se convierte en el denominador de una fracción por separado. Luego ponga incógnitas en el numerador de cada fracción.
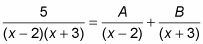
Multiplicar ambos lados de esta ecuación por el denominador del lado izquierdo.
Este es el álgebra I, lo que no puede desear para ver los pasos. ¿Correcto?
5 = LA(X + 3) + B(X - 2)
Tome las raíces de los factores lineales y conectarlos - uno a la vez - en X en la ecuación de la Etapa 3, y resolver las incógnitas.
Si X = 2
5 = LA(2 + 3) + B(2 - 2)
5 = 5LA
LA = 1
O si X = -3
5 = LA(-3 + 3) + B(-3 - 2)
5 = -5B
B = -1
Conecte estos resultados en el LA y B en la ecuación de la Etapa 2.
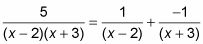
Dividir la integral original en las fracciones parciales desde el paso 5 y estás en casa gratis.
¿Cómo aumentar los términos de una fracción Incluso si se ven diferentes fracciones, que en realidad puede representar la misma cantidad- en otras palabras, una de las fracciones habrá aumentado términos en comparación con el otro. Puede que tenga que aumentar los términos de las…
Cómo restar fracciones con el mismo denominador Restar fracciones con el mismo denominador (número inferior) es fácil. Cuando los denominadores son los mismos, sólo puede pensar en las fracciones como pedazos de torta.Para restar una fracción de otro cuando ambos tienen el mismo denominador,…
Cómo descomponer fracciones parciales Un proceso llamado fracciones parciales toma un fracción y la expresa como la suma o diferencia de otras dos fracciones. En cálculo, este proceso es útil antes de integrar una función. Debido a que la integración es mucho más fácil cuando el…
Descomponer fracciones parciales en 8 pasos Cuando su instructor de pre-cálculo le pide que para descomponer fracciones parciales, que en realidad no es tan complicado como parece. El proceso de descomponer una fracción parcial requiere para separar la fracción en dos fracciones (o a veces…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede…
Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles A veces no se puede factorizar un denominador todo el camino a factores lineales porque algunas ecuaciones cuadráticas son irreductibles - al igual que los números primos, no pueden tenerse en cuenta.Comprobar el discriminante. Puede comprobar…
La creación de fracciones parciales cuando se ha repetido factores lineales Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores lineales…
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…
La creación de fracciones parciales cuando tiene distintos factores Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es cuando el denominador es el…
Preparación ASVAB: cómo sumar y restar fracciones Adición y sustracción de fracciones para el ASVAB (o para cualquier otro propósito) puede ser tan simple como multiplicar y dividir, o puede ser más difícil. A medida que la siguiente información muestra, todo depende de si las fracciones…
Preparación ASVAB: cómo comparar fracciones Los dos subpruebas de matemáticas del ASVAB preguntan a menudo que usted pueda comparar fracciones para determinar cuál es la más grande o más pequeño. Si las fracciones tienen el mismo denominador, es fácil. La fracción con el mayor…