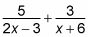Descomponer fracciones parciales en 8 pasos
Cuando su instructor de pre-cálculo le pide que para descomponer fracciones parciales, que en realidad no es tan complicado como parece. El proceso de descomponer una fracción parcial requiere para separar la fracción en dos fracciones (o a veces más) inconexas con las variables (por lo general A, B, C, y así sucesivamente) de pie en como marcadores de posición en el numerador. A continuación, puede establecer un sistema de ecuaciones para resolver estas variables.
El proceso de pfracciones artial toma un fracción y la expresa como la suma o diferencia de dos o más de otras fracciones. Hay muchas razones por las que había necesidad de hacerlo. En cálculo, este proceso es útil antes de integrar una función. Debido a que la integración es mucho más fácil cuando el grado de una función racional es 1 en el denominador, la fracción de la descomposición parcial es una herramienta útil para usted.
Ahora trata de un ejemplo. Digamos que usted necesita para escribir la descomposición en fracciones parciales de la siguiente fracción:
Para ello, debería seguir estos pasos:
Factorizar el denominador y reescribir como LA más de un factor y B sobre el otro.
Esto se hace porque quiere romper la fracción en dos. El proceso se desarrolla de la siguiente manera:
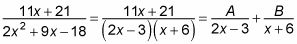
Multiplica cada término que has creado por el denominador factorizada y luego cancela.
Usted multiplica un total de tres veces en este ejemplo:
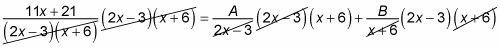
Esta expresión es igual a lo siguiente:
11x + 21 = A (x + 6) + B (2x - 3)
Distribuir LA y B.
Este paso le da
11x + 21 = Ax + 6A + 2Bx - 3B
En el lado derecho de la ecuación única, ponga todos los términos con un X juntos y todos los términos sin juntos.
Reorganizar le da
11x + 21 = Ax + 2Bx + 6A - 3B
Factorizar el X a partir de los términos en el lado derecho.
Ahora tiene
11X + 21 = (LA + 2B)X + 6LA - 3B
Crear un sistema de esta ecuación haciendo pares términos.
Para una ecuación para trabajar, todo debe estar en equilibrio. Debido a este hecho, los coeficientes de X deben ser iguales y las constantes deben ser iguales. Si el coeficiente de X es 11 a la izquierda y LA + 2B a la derecha, se puede decir que 11 = LA + 2B es una ecuación. Las constantes son los términos con ninguna variable, y en este caso, la constante de la izquierda es 21. En el lado derecho, 6LA - 3B es la constante (porque ninguna variable se adjunta) y así 21 = 6LA - 3B.
Resuelve el sistema, utilizando la sustitución o eliminación.
En este ejemplo, vamos a usar la eliminación. Dispone de las siguientes ecuaciones:
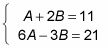
Así que usted puede multiplicar la ecuación por encima -6 y luego añadir eliminar y resolver. Usted encontrará que LA = 5 y B = 3.
Escribe la solución como la suma de dos fracciones.
Cómo restar fracciones con el mismo denominador Restar fracciones con el mismo denominador (número inferior) es fácil. Cuando los denominadores son los mismos, sólo puede pensar en las fracciones como pedazos de torta.Para restar una fracción de otro cuando ambos tienen el mismo denominador,…
En fracciones, uno es el número más fácil Con fracciones, la relación entre los números, no los números reales en sí, es más importante. Comprender cómo multiplicar y dividir fracciones pueden darle una comprensión más profunda de por qué se puede aumentar o disminuir los números…
Cómo descomponer fracciones parciales Un proceso llamado fracciones parciales toma un fracción y la expresa como la suma o diferencia de otras dos fracciones. En cálculo, este proceso es útil antes de integrar una función. Debido a que la integración es mucho más fácil cuando el…
¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales Usted puede utilizar el método de fracciones parciales para integrar funciones racionales (Recordemos que una función racional es uno polinomio dividido por otro.) La idea básica detrás del enfoque de fracciones parciales es " unadding " una…
La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede…
Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles A veces no se puede factorizar un denominador todo el camino a factores lineales porque algunas ecuaciones cuadráticas son irreductibles - al igual que los números primos, no pueden tenerse en cuenta.Comprobar el discriminante. Puede comprobar…
La creación de fracciones parciales cuando se ha repetido factores lineales Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores lineales…
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…
La creación de fracciones parciales cuando tiene distintos factores Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es cuando el denominador es el…
Sistemas de ecuaciones utilizadas en pre-cálculo LA sistema de ecuaciones es una colección de dos o más ecuaciones que implican dos o más variables. Si el número de ecuaciones es igual al número de variables diferentes, entonces usted puede ser capaz de encontrar una solución única que es…
Romper o combinar fracciones para resolver una identidad trigonometría Una identidad trigonométrica con fracciones puede trabajar a su ventaja- te dan una plan de ataque. Usted puede trabajar hacia la eliminación de la fracción y, en el proceso, resolver el problema. Dos de las principales técnicas para trabajar…
Preparación ASVAB: cómo sumar y restar fracciones Adición y sustracción de fracciones para el ASVAB (o para cualquier otro propósito) puede ser tan simple como multiplicar y dividir, o puede ser más difícil. A medida que la siguiente información muestra, todo depende de si las fracciones…