La creación de fracciones parciales cuando tiene distintos factores
Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es cuando el denominador es el producto de distinto
Conteúdo
Para cada factor cuadrático distinta en el denominador, añada una fracción parcial de la siguiente forma:
Por ejemplo, suponga que desea integrar esta función:
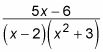
El primer factor en el denominador es lineal, pero la segunda es cuadrática y no puede ser descompuesto a factores lineales. Así que configurar sus fracciones parciales de la siguiente manera:
El número de factores cuadráticos distintas en el denominador le indica cuántas fracciones parciales que se obtiene. Así, en este ejemplo, dos factores en el denominador producen dos fracciones parciales.
Trabajar sistemáticamente con un sistema de ecuaciones
La creación de un sistema de ecuaciones es un método alternativo para encontrar el valor de incógnitas cuando se está trabajando con fracciones parciales. No es tan simple como conectar las raíces de los factores, pero es su única opción cuando la raíz de un factor de segundo grado es imaginario.
Aquí hay un problema para ilustrar este método:
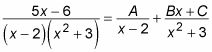
Para empezar, ver hasta dónde se puede obtener mediante la conexión de las raíces de ecuaciones. Comience por conseguir un denominador común en el lado derecho de la ecuación:
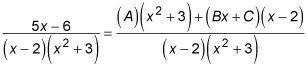
Ahora multiplique toda la ecuación por el denominador:
5X - 6 = (LA) (X2 + 3) + (Bx + C) (X - 2)
La raíz de X - 2 es 2, así que vamos a X = 2 y ver lo que se obtiene:
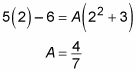
Ahora usted puede sustituir
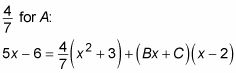
Desafortunadamente, X2 + 3 tiene raíz en los números reales, por lo que necesita un enfoque diferente. En primer lugar, deshacerse de los paréntesis en el lado derecho de la ecuación:
A continuación, combinar términos similares (usando X como la variable por el cual se juzga similitud). Esto es sólo el álgebra:
Debido a esta ecuación funciona para todas valores de X, ahora toma lo que parece ser un paso cuestionable, rompiendo esta ecuación en tres ecuaciones independientes de la siguiente manera:
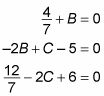
En este punto, un poco de álgebra te dice que
Así que usted puede sustituir los valores de LA, B, y C de nuevo en las fracciones parciales:
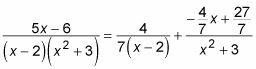
Puede simplificar la segunda fracción un poco:
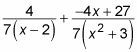
Factores cuadráticas de la forma (hacha2 + C)
Cuando usted comienza con un factor de segundo grado de la forma (hacha2 + C), Usando fracciones parciales se traduce en las siguientes dos integrales:
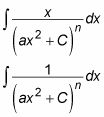
Integrar el primero mediante la sustitución de variables u = hacha2 + C así que eso du = 2hacha dx y
Esta sustitución da como resultado la siguiente integral:
Aquí hay unos ejemplos:
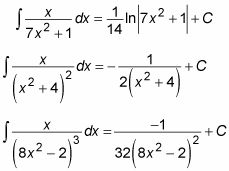
Para evaluar la segunda integral, utilice la siguiente fórmula:
Factores cuadráticas de la forma (hacha2 + bx + C)
La mayoría de los profesores de matemáticas tienen al menos una pizca de misericordia en sus corazones, para que no tienden a darle problemas que incluyen este caso más difícil. Cuando usted comienza con un factor de segundo grado de la forma (hacha2 + bx + C), Usando fracciones parciales se traduce en la siguiente integral:
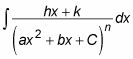
Bueno, eso es demasiado muchas cartas y no casi suficientes números. He aquí un ejemplo:
Se trata de la integrante más peludo alguna vez va a ver en el otro extremo de una fracción parcial. Para evaluarlo, desea utilizar la sustitución de variables u = X2 + 6X + 13 de manera que du = (2X + 6) dx. Si el numerador eran 2X + 6, estarías en gran forma. Así que hay que ajustar el numerador un poco. Primero se multiplica por 2 y dividir toda la integral por 2:
Porque multiplicado toda la integral por 1, se ha producido ningún cambio neto. Ahora agregue 6 y -6 al numerador:
Usted ha añadido 0 a la integral, que no cambió su valor. En este punto, se puede dividir la integral en dos:
En este punto, puede utilizar la sustitución de variables para cambiar el primer integrante de la siguiente manera:
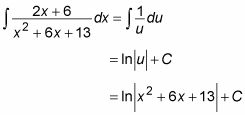
Para resolver la segunda integral, completa el cuadrado en el denominador: Divida la b plazo (6) por 2 y de la plaza, y luego representar el C plazo (13) como la suma de esto y todo lo que queda:
Ahora dividir el denominador en dos cuadrados:
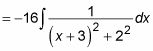
Para evaluar esta fórmula integral uso se muestra en la sección anterior:
Así que aquí está la respuesta final para la segunda integral:
Por lo tanto, reconstruir la respuesta completa de la siguiente manera:
Cómo reducir una fracción a su mínima expresión Incluso si se ven diferentes fracciones, que en realidad puede representar la misma cantidad- en otras palabras, una de las fracciones habrá reducido términos en comparación con el otro. Puede que tenga que reducir los términos de las fracciones…
Cómo restar fracciones con el mismo denominador Restar fracciones con el mismo denominador (número inferior) es fácil. Cuando los denominadores son los mismos, sólo puede pensar en las fracciones como pedazos de torta.Para restar una fracción de otro cuando ambos tienen el mismo denominador,…
Cómo descomponer fracciones parciales Un proceso llamado fracciones parciales toma un fracción y la expresa como la suma o diferencia de otras dos fracciones. En cálculo, este proceso es útil antes de integrar una función. Debido a que la integración es mucho más fácil cuando el…
Descomponer fracciones parciales en 8 pasos Cuando su instructor de pre-cálculo le pide que para descomponer fracciones parciales, que en realidad no es tan complicado como parece. El proceso de descomponer una fracción parcial requiere para separar la fracción en dos fracciones (o a veces…
¿Cómo distinguir expresiones racionales propias e impropias Integración por fracciones parciales sólo funciona con expresiones racionales adecuadas, pero no con expresiones racionales impropias. Decirle a una fracción propia a partir de uno inadecuada es fácil: Una fracción a / b es correcta si el…
¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales Usted puede utilizar el método de fracciones parciales para integrar funciones racionales (Recordemos que una función racional es uno polinomio dividido por otro.) La idea básica detrás del enfoque de fracciones parciales es " unadding " una…
La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede…
Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles A veces no se puede factorizar un denominador todo el camino a factores lineales porque algunas ecuaciones cuadráticas son irreductibles - al igual que los números primos, no pueden tenerse en cuenta.Comprobar el discriminante. Puede comprobar…
La creación de fracciones parciales cuando se ha repetido factores lineales Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores lineales…
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…
La creación de fracciones parciales cuando se ha repetido factores cuadráticos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. Uno de los casos donde se puede utilizar fracciones parciales es con factores cuadráticos…
Preparación ASVAB: cómo sumar y restar fracciones Adición y sustracción de fracciones para el ASVAB (o para cualquier otro propósito) puede ser tan simple como multiplicar y dividir, o puede ser más difícil. A medida que la siguiente información muestra, todo depende de si las fracciones…