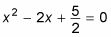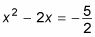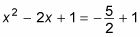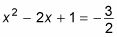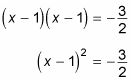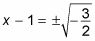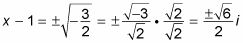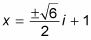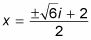Cómo completar el cuadrado
Completando la plaza es muy útil cuando se le pide que resolver una ecuación cuadrática unfactorable y cuando es necesario para representar gráficamente las secciones cónicas (círculos, elipses, parábolas e hipérbolas).
Sólo debe encontrar las raíces de una cuadrática utilizando esta técnica cuando se le pide específicamente que lo haga, porque factorizar un cuadrática y utilizando la fórmula cuadrática trabajo igual de bien (si no mejor). Esos métodos son menos complicados que completar el cuadrado (un dolor en el ya-sabes-donde!).
Por ejemplo, si su instructor pide a resolver la ecuación 2X2 - 4X + 5 = 0, puede hacerlo completando el cuadrado:
Divida cada término por el coeficiente principal de manera que la = 1.
Si la ecuación tiene ya una llanura X2 plazo, puede saltar al paso 2.
Esté preparado para hacer frente a las fracciones en este paso. Al dividir cada término por 2, la ecuación se convierte ahora
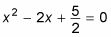
Restar el término constante de ambos lados de la ecuación para obtener sólo con la variable de términos en el lado izquierdo de la ecuación.
Puede restar 2/5 de ambas partes para llegar
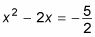
Ahora, para completar la plaza: Se divide el coeficiente lineal por 2 y escribir a continuación el problema para más adelante, cuadrar esta respuesta, y luego añadir ese valor a ambos lados para que ambas partes siguen siendo iguales.
Divida -2 por 2 para obtener -1. Cuadrar esta respuesta para obtener 1, y agregarlo a ambos lados:
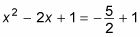
Simplifique la ecuación.
La ecuación se convierte en
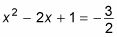
Factor de la ecuación de segundo grado de nueva creación.
La nueva ecuación debe ser un trinomio cuadrado perfecto.
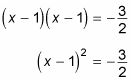
Deshágase del exponente plaza tomando la raíz cuadrada de ambos lados.
Recuerde que las raíces positivas y negativas podrían ser ambos al cuadrado para obtener la respuesta! Este paso le da
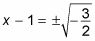
Simplifique las raíces cuadradas, si es posible.
El ejemplo ecuación no simplifica, pero la fracción es imaginario y el denominador debe ser racionalizado. Hacer el trabajo de conseguir
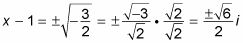
Resolver para la variable aislándolo.
Se agrega 1 a ambos lados para obtener
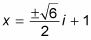
Nota: Se le puede pedir para expresar su respuesta como uno fraccionamiento en este caso, encontrar el denominador común y agregar a conseguir
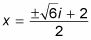
Sobre el autor
 Encontrar las raíces de una ecuación factorizada
Encontrar las raíces de una ecuación factorizada En pre-cálculo, puede utilizar la propiedad del producto cero a encontrar las raíces de una ecuación factorizada. Después se toma un polinomio en sus diferentes piezas, puede configurar cada pieza igual a cero para resolver las raíces con la…
 ¿Cómo combinar los ángulos de referencia con otras técnicas para resolver ecuaciones trigonométricas
¿Cómo combinar los ángulos de referencia con otras técnicas para resolver ecuaciones trigonométricas Puede incorporar ángulos de referencia en algunas otras técnicas de pre-cálculo para resolver ecuaciones trigonométricas. Una de estas técnicas es el factoring. Usted ha estado factoring desde álgebra, por lo que este proceso no debe ser nada…
 ¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados
¿Cómo resolver una ecuación exponencial con una variable en uno o ambos lados Ya sea una ecuación exponencial contiene una variable en uno o ambos lados, el tipo de ecuación se le pide resolver determina los pasos que se dan para resolverlo.El tipo básico de la ecuación exponencial tiene una variable en un solo lado y se…
 ¿Cómo resolver una ecuación exponencial tomando el logaritmo de ambos lados
¿Cómo resolver una ecuación exponencial tomando el logaritmo de ambos lados A veces usted no puede expresar ambos lados de una ecuación exponencial como potencias de la misma base. Al hacer frente a ese problema, puede hacer que el exponente se vaya tomando el logaritmo de ambos lados. Por ejemplo, supongamos que se le…
 ¿Cómo resolver (y el factor) una ecuación cuadrática con la fórmula cuadrática
¿Cómo resolver (y el factor) una ecuación cuadrática con la fórmula cuadrática Una ecuación cuadrática es cualquier segundo grado ecuación polinómica - que es cuando la mayor potencia de X, o cualquier otra variable se usa, es de 2. La solución o soluciones de una ecuación de segundo grado,Resolver la ecuación,con la…
 ¿Cómo resolver una ecuación cuadrática cuando no lo hará factor de
¿Cómo resolver una ecuación cuadrática cuando no lo hará factor de Cuando se le preguntó a resolver una ecuación cuadrática que usted apenas no puede parecerse al factor (o que simplemente no hace de los factores), hay que emplear otras formas de resolver la ecuación, como mediante el uso de la fórmula…
 ¿Cómo resolver una ecuación cuadrática completando el cuadrado
¿Cómo resolver una ecuación cuadrática completando el cuadrado Puede resolver ecuaciones de segundo grado por completando el cuadrado. Completando la plaza implica la creación de un trinomio cuadrado perfecto de la ecuación de segundo grado, y luego resolver ese trinomio mediante la adopción de su raíz…
 ¿Cómo resolver sistemas no lineales
¿Cómo resolver sistemas no lineales En un sistema no lineal, al menos una ecuación tiene una gráfica que no es una línea recta - es decir, al menos una de las ecuaciones tiene que ser no lineal. Su instructor de pre-cálculo le dirá que siempre se puede escribir una ecuación…
 Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles
Integrar las funciones donde el denominador contiene factores cuadráticos irreducibles A veces no se puede factorizar un denominador todo el camino a factores lineales porque algunas ecuaciones cuadráticas son irreductibles - al igual que los números primos, no pueden tenerse en cuenta.Comprobar el discriminante. Puede comprobar…
 Cómo cuadrar ambos lados de una ecuación trigonométrica
Cómo cuadrar ambos lados de una ecuación trigonométrica Cuando la resolución de ecuaciones de trigonometría, más de un método generalmente funciona - a pesar de un método es a menudo más rápido o más fácil que otro. Con la práctica, usted obtendrá buenos en la elección de la mejor de las…
 Preparación ASVAB: cómo resolver ecuaciones cuadráticas
Preparación ASVAB: cómo resolver ecuaciones cuadráticas Ecuaciones cuadráticas probablemente aparecerá en la ASVAB.A ecuación cuadrática es una ecuación algebraica en la que el desconocido se eleva a un exponente no superior a 2, como en X2. Pueden ser (grados o varios de dificultad entre los dos)…
 Preparación núcleo Praxis: cómo resolver para x y otras variables
Preparación núcleo Praxis: cómo resolver para x y otras variables Tendrá que ser capaz de resolver para x (o cualquier variable) en el examen Praxis Core. Resolución de ecuaciones es una parte enorme de álgebra. La comprensión de cómo hacerlo te pone en una excelente posición para conquistar Praxis Core…