Cómo evaluar una integral impropia que es horizontalmente infinita
Integrales impropias son útiles para resolver una variedad de problemas. LA horizontalmente infinita integral impropia contiene ya sea # 8734- o - # 8734- (o ambos) como un límite de la integración.
Evaluación de una integral impropia es un proceso de tres pasos:
Expresar la integral impropia como el límite de un integrante adecuada.
Evaluar la integral por cualquier método funciona.
Evaluar el límite.
Una integral impropia horizontal se produce cuando una integral definida tiene un límite de integración que es ya sea # 8734- o - # 8734-. Este tipo de integral impropia es fácil de detectar porque el infinito es allí mismo, en la propia integral. Usted no podrá pasarlo de largo.
Por ejemplo, suponga que desea evaluar la siguiente integral impropia:
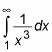
He aquí cómo lo haces, paso a paso:
Expresar la integral impropia como el límite de un integrante adecuada.
Cuando el límite superior de integración es # 8734-, utilice esta ecuación:
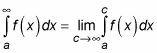
Así que aquí es lo que haces:
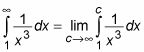
Evaluar la integral:
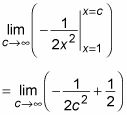
Evaluar el límite:
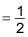
Antes de continuar, reflexionar por un momento que el área bajo una infinitamente larga curva es en realidad finito. Ah, la magia y el poder de cálculo!
Del mismo modo, supongamos que usted desea evaluar lo siguiente:
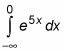
He aquí cómo se hace:
Expresar la integral como el límite de un integrante adecuada.
Cuando el límite inferior de integración es - # 8734-, utilice esta ecuación:
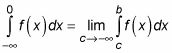
Así que aquí está lo que usted escribe:
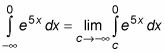
Evaluar la integral:
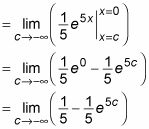
Evaluar el límite - en este caso, como c se acerca - # 8734-, el primer término no se ve afectada y el segundo término se aproxima a 0:
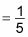
Una vez más, el cálculo le indica que, en este caso, el área bajo una curva infinitamente larga es finito.
Por supuesto, a veces el área bajo una curva infinitamente largo es infinito. En estos casos, la integral impropia no puede ser evaluada debido a que el límite no existe (DNE). Aquí está un ejemplo rápido que ilustra esta situación:
Puede que no sea obvio que esta integral impropia representa un área infinitamente grande. Después de todo, el valor de la función se aproxima a 0 como X aumenta. Pero ten cuidado con cómo esta evaluación juega:
Expresar la integral impropia como el límite de un integrante adecuado:
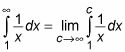
Evaluar la integral:
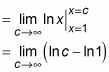
En este punto, se puede ver que el límite explota hasta el infinito, por lo que no existe. Por lo tanto, la integral impropia no puede ser evaluada, debido a que el área que representa es infinito.
-
Evaluar una integral definida en la TI-83 Plus -
Evaluar una integral definida con la TI-84 Plus -
Comando Integral de TI-Nspire submenú cálculo cas -
Cómo convertir una fracción impropia a un número mixto -
La determinación de si una serie converge utilizando la prueba de comparación integral -
Evaluación de límites en el cálculo
La evaluación de las integrales dobles Integrales dobles suelen ser integrales definidas, por lo que la evaluación de los resultados en un número real. La evaluación de las integrales dobles es similar a la evaluación de funciones anidadas: Usted trabaja de adentro hacia afuera.Puede…
La evaluación de las integrales triples Integrales triples son generalmente integrales definidas, por lo que la evaluación de los resultados en un número real. La evaluación de las integrales triples es similar a la evaluación de funciones anidadas: Usted trabaja de adentro hacia…
Encuentra la integral de funciones anidadas A veces es necesario integrar una función que es la composición de dos funciones - por ejemplo, la función 2X anidada dentro de una función seno. Si estaba diferenciando, se puede utilizar la regla de la cadena. Desafortunadamente, no existe una…
Cómo evaluar una integral impropia que es verticalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…
¿Cómo integrar una serie de potencias Debido a la serie de potencia se asemejan polinomios, son fáciles de integrar el uso de un proceso de tres pasos simples que utiliza la regla de la suma, la Regla múltiplo constante, y la Regla de energía.Por ejemplo, echar un vistazo a la…
Cómo hacer inaceptables formas aceptables antes de usar l'h & # regla del 244-pital Usted puede utilizar la regla de L'H # de 244-pital de encontrar un límite cuando otros métodos no funcionan. De hecho, incluso si algún otro método funciona, regla de L'H # de 244-pital es a menudo un buen atajo. Si la sustitución del número…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver integrales impropias de funciones que tienen asíntotas verticales A resolver integrales impropias, al convertirlos en problemas de límite. No se puede hacer de ellos la manera regular. He aquí cómo resolver integrales impropias de funciones que tienen asíntotas verticales. Hay dos casos: una asíntota vertical…
¿Cómo resolver integrales impropias que tienen uno o dos límites infinitos de integración Una de las formas en que pueden ser integrales definidas inadecuada es cuando uno o ambos de los límites de integración son infinitas. A resolver este tipo de integral impropia al convertirlo en un problema de límite en c tiende a infinito o…
Cómo dividir una integral definida en dos integrales definidas Cuando la solución de problemas de la zona, a veces es necesario dividir una integral en dos integrales definidas separadas. Aquí hay una regla simple, pero muy útil para hacer esto que parece complicado, pero es realmente muy fácil:Esta regla…
Cómo utilizar la integración por partes Al hacer Cálculo, la fórmula de integración por partes te da la opción de romper el producto de dos funciones a sus factores e integrarlo en una forma alterada. Para utilizar la integración por partes en cálculo, siga estos pasos:Descomponer…
La medición de volumen bajo una superficie usando una integral doble Una integral doble le permite medir el volumen bajo una superficie tan limitada por un rectángulo. Integrales definidas proporcionan una forma confiable de medir el área firmado entre una función y la X-eje como limitada por cualquiera de los dos…