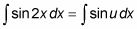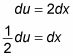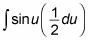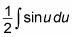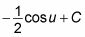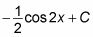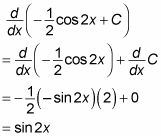Encuentra la integral de funciones anidadas
A veces es necesario integrar una función que es la composición de dos funciones - por ejemplo, la función 2X anidada dentro de una función seno. Si estaba diferenciando, se puede utilizar la regla de la cadena. Desafortunadamente, no existe una regla de la cadena para la integración.
Afortunadamente, una función tal como
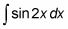
es un buen candidato para la sustitución de variables. Sigue estos pasos:
Declarar una variable nueva u como sigue y sustituir en la integral:
Dejar u = 2X
Ahora sustituir u para 2X como sigue:
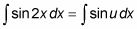
Esto puede verse como la respuesta a todos sus problemas, pero usted tiene un problema más para resolver. Tal como está, el símbolo dx le dice que la variable de integración sigue siendo X.
Para integrar correctamente, es necesario encontrar una manera de cambiar dx a una expresión que contiene du. Eso es lo que los pasos 2 y 3 están a punto.
Diferenciar la función u = 2X.
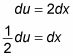
Sustituto mediadu para dx en la integral:
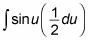
Usted puede tratar el medio como cualquier coeficiente y utilizar la Regla múltiple Constante para llevarlo fuera de la integral:
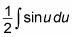
En este punto, usted tiene una expresión que usted sabe cómo evaluar:
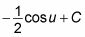
Ahora que la integración se lleva a cabo, el último paso es sustituir 2X copias por u:
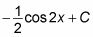
Puede comprobar esta solución mediante la diferenciación mediante la regla de la cadena:
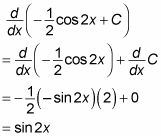
Sobre el autor
 Cómo antidifferentiate cualquier polinomio utilizando la suma, constante múltiple, y las reglas de alimentación
Cómo antidifferentiate cualquier polinomio utilizando la suma, constante múltiple, y las reglas de alimentación Las reglas anti-diferenciación para la integración en gran medida limitar el número de integrales se puede calcular fácilmente. En muchos casos, sin embargo, puede integrar alguna polinomio en tres pasos utilizando la regla de la suma, la Regla…
 ¿Cómo integrar una serie de potencias
¿Cómo integrar una serie de potencias Debido a la serie de potencia se asemejan polinomios, son fáciles de integrar el uso de un proceso de tres pasos simples que utiliza la regla de la suma, la Regla múltiplo constante, y la Regla de energía.Por ejemplo, echar un vistazo a la…
 ¿Cómo integrar una función multiplicada por un conjunto de funciones anidadas
¿Cómo integrar una función multiplicada por un conjunto de funciones anidadas A veces es necesario integrar el producto de una función (X) Y una composición de funciones (por ejemplo, la función 3X2 + 7 anidada dentro de una función de raíz cuadrada). Si estaba diferenciando, podría utilizar una combinación de la regla…
 ¿Cómo integrar composiciones de funciones
¿Cómo integrar composiciones de funciones Las composiciones de funciones - es decir, una función anidada dentro de otra - son de la forma F(g(X)). Usted puede integrarlos sustituyendo u = g(X) cuandoUsted sabe cómo integrar la función externa F.La función interna g(X) diferencia a una…
 ¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de seno
¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de seno He aquí cómo usted integra un integrante trig que contiene senos y cosenos, donde el poder de seno es impar y positivo. Usted cortar un factor sine y ponerlo a la derecha del resto de la expresión, convertir los restantes (incluso) factores seno…
 ¿Cómo integrar expresiones racionales utilizando la suma, constante múltiple, y las reglas de alimentación
¿Cómo integrar expresiones racionales utilizando la suma, constante múltiple, y las reglas de alimentación En muchos casos, puede desenredar expresiones racionales peludas e integrarlos utilizando las reglas anti-diferenciación más la regla de la suma, la Regla múltiplo constante, y la Regla de energía.La regla de la suma para la integración le dice…
 ¿Cómo integrar potencias pares de senos y cosenos
¿Cómo integrar potencias pares de senos y cosenos Puede integrar poderes incluso de senos y cosenos. Por ejemplo, si desea integrar el pecado2 X y cos2 X, que utilizaría estas identidades trigonométricas dos semi-ángulo:He aquí cómo usted integra cos2 X:Utilice la identidad-medio ángulo para…
 ¿Cómo resolver integrales con la sustitución de variables
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
 Cómo utilizar la integración por partes
Cómo utilizar la integración por partes Al hacer Cálculo, la fórmula de integración por partes te da la opción de romper el producto de dos funciones a sus factores e integrarlo en una forma alterada. Para utilizar la integración por partes en cálculo, siga estos pasos:Descomponer…
 Cómo utilizar la regla de la cadena para encontrar la derivada de funciones anidadas
Cómo utilizar la regla de la cadena para encontrar la derivada de funciones anidadas A veces, cuando lo que necesita para encontrar la derivada de una función anidada con la regla de la cadena, averiguar qué función está dentro de lo que puede ser un poco difícil - especialmente cuando una función está anidado dentro de otro…
 Saber cuándo integrar por partes
Saber cuándo integrar por partes Es importante reconocer que la integración por partes es útil. Para empezar, aquí hay dos casos importantes cuando la integración por partes es definitivamente el camino a seguir:La función logarítmica ln XLas cuatro primeras funciones…
 La creación de fracciones parciales cuando se tiene factores lineales distintos
La creación de fracciones parciales cuando se tiene factores lineales distintos Su primer paso en cualquier problema que involucra fracciones parciales es reconocer cuyo caso usted está tratando con lo que pueda solucionar el problema. El caso más simple en el que las fracciones parciales son útiles es cuando el denominador…