Cómo utilizar la regla de la cadena para encontrar la derivada de funciones anidadas
A veces, cuando lo que necesita para encontrar la derivada de una función anidada con la regla de la cadena, averiguar qué función está dentro de lo que puede ser un poco difícil - especialmente cuando una función está anidado dentro de otro y luego ambos son dentro de una tercera función ( usted puede tener cuatro o más funciones anidadas, pero tres es probablemente el más verás).
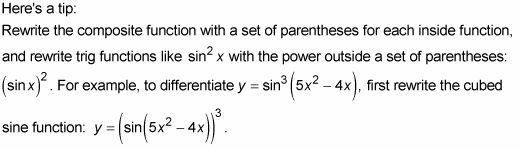
Ahora es fácil ver el orden en el que las funciones están anidadas. La función más interna es dentro de los paréntesis más internos - que es
A continuación, la función seno está dentro del siguiente conjunto de paréntesis - que está
pecado(cosas)
Por último, la función de medición de volumen está en el exterior de todo - que está cosas3
Bien, ahora que usted sabe el orden de las funciones, se puede diferenciar de afuera en.
La función más externa es cosas en cubos y su derivado está dada por la regla de la potencia.
Al igual que con todos los problemas de la regla de la cadena, usted multiplica eso por stuff '.
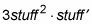
Pon el cosas,
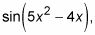
de vuelta a donde pertenece.
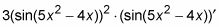
Use la regla de la cadena de nuevo.
los cosas es
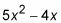
y su derivado es 10X - 4. Conecte las cosas de nuevo.
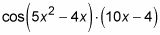
Ahora que usted tiene la derivada de
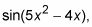
conecte este resultado en el resultado del paso 3, que le da toda la enchilada.
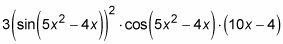
Esto se puede simplificar un poco.
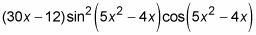
Puede haber ocurrido que usted puede ahorrar un poco de tiempo al no cambiar a la palabra cosas y luego cambiar de nuevo. Eso es cierto, pero las fuerzas de la técnica que usted deje la cosas solo durante cada paso de un problema. Ese es el punto crítico. Asegúrese de no tocar las cosas.
-
Comando Derivada de TI-Nspire submenú cálculo cas -
Reglas de cálculo básicas para la economía de la empresa -
Cálculo: cómo resolver los problemas de diferenciación -
Calcular las integrales y representando integrales como funciones -
Encontrar la integral de un producto de dos funciones -
Encuentra la integral de funciones anidadas
¿Cómo diferenciar las funciones exponenciales y logarítmicas Diferenciar las funciones exponenciales y logarítmicas implica reglas especiales. No se preocupe - una vez que memorizar un par de reglas, diferenciando estas funciones es un pedazo de pastel.Las funciones exponenciales: Si no puede memorizar esta…
¿Cómo diferenciar funciones inversas Hay una fórmula difícil buscar la participación de las derivadas de las funciones inversas, pero antes de llegar a eso, a ver la figura siguiente, que resume muy bien la idea.Esta cifra muestra un par de funciones inversas, F y g. Funciones…
¿Cómo diferenciar implícitamente A veces se le pide para diferenciar una ecuación que no está resuelto por y, como y5 + 3X2 = Sen X - 4y3. Esta ecuación define y de forma implícita como una función de X, y no se puede escribir como una función explícita porque no puede ser…
¿Cómo encontrar derivada de una función mediante el uso de la regla de la cadena La regla de la cadena es de lejos la regla derivada más difícil, pero en realidad no es tan malo si se concentra con cuidado sobre algunos puntos importantes.Por cierto, aquí es una manera de reconocer rápidamente una función compuesta.Cada vez…
¿Cómo encontrar primitivas utilizando reglas inversas Puede utilizar las reglas inversas para encontrar primitivas. Las más sencillas reglas antiderivada son los que son lo contrario de las normas derivadas que ya conoce. Estos son, primitivas automáticos de un solo paso con la excepción de la regla…
¿Cómo encontrar primitivas con el método de sustitución Cuando el argumento de una función (que es la entrada de la función) es más complicado que algo así como 3X + 2 (a lineal funcion de X - es decir, una función donde X se eleva a la primera potencia), puede utilizar el método de sustitución.…
¿Cómo encontrar derivados utilizando las normas de productos y cocientes Hay reglas especiales para encontrar la derivada del producto de dos funciones o el cociente de dos funciones- estos son la regla del producto y de la regla del cociente, respectivamente.Estado del producto: Se utiliza la regla del producto para -…
¿Cómo encontrar derivados de alto orden Encontrar un segundo, tercero, cuarto, o superior derivado es increíblemente simple. La segunda derivada de una función es simplemente la derivada de su primera derivada. La tercera derivada es la derivada de la segunda derivada, el cuarto…
¿Cómo encontrar los números críticos de una función Todos los extremos locales se producen en los puntos críticos de una función - que es donde la derivada es cero o indefinido (pero no se olvide que los puntos críticos no siempre son extremos locales). Así, el primer paso en la búsqueda de…
¿Cómo integrar una función multiplicada por un conjunto de funciones anidadas A veces es necesario integrar el producto de una función (X) Y una composición de funciones (por ejemplo, la función 3X2 + 7 anidada dentro de una función de raíz cuadrada). Si estaba diferenciando, podría utilizar una combinación de la regla…
¿Cómo saber cuando un derivado no existe Hay tres situaciones en las que un derivado de falla de existir. La derivada de una función en un punto dado es la pendiente de la recta tangente en ese punto. Por lo tanto, si no se puede trazar una línea tangente, no hay derivada - que sucede en…
Resolver funciones compuestos donde la función interna es hacha Al calcular problemas de Cálculo, algunas integrales de funciones compuestos F (g(X)) Son fáciles de hacer rápidamente. Estos incluyen funciones compuestos para los que saben cómo integrar la función externa F, y la función interna g(X) Es de…