¿Cómo diferenciar implícitamente
A veces se le pide para diferenciar una ecuación que no está resuelto por y, como y5 + 3X2 = Sen X - 4y3. Esta ecuación define y de forma implícita como una función de X, y no se puede escribir como una función explícita porque no puede ser resuelto por y. Para este problema, es necesario diferenciación implícita. Cuando la diferenciación implícita, todas las reglas derivadas funcionan de la misma, con una excepción: cuando a diferenciar un término con una y en ella, se utiliza la regla de la cadena con un pequeño giro.
Por ejemplo, puede utilizar la regla de la cadena para diferenciar algo así como el pecado (X3) De la siguiente manera: comenzar con la función de fuera, el pecado, y diferenciar que, ignorando lo que hay dentro - en este caso, X3. Para asegurarse de que usted ignora el interior, reemplace temporalmente la función de interior con la palabra cosas. En este ejemplo, el derivado de seno es coseno, por lo que la derivada de sen (cosas) es
Terminas el problema mediante la búsqueda de la derivada de la cosas, X3, que es 3X2, y luego hacer las sustituciones para darle
Con la diferenciación implícita, una y funciona como la palabra cosas. Por lo tanto, debido
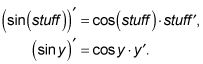
El giro es que mientras que la palabra cosas está tomando temporalmente el lugar de algunos conocido funcion de X (X3 en este ejemplo), y es cierto desconocido funcion de X (usted no sabe lo que el y iguales en términos de X). Y porque usted no sabe lo que y iguales, la y y el
Pero el concepto es exactamente lo mismo, y te tratan y al igual que el cosas. Usted simplemente no puede hacer el cambio de nuevo a Xs al final del problema como usted puede con un problema regular de regla de la cadena.
He aquí un ejemplo. Diferenciar y5 + 3X2 = Sen X - 4y3:
Diferenciar cada término en ambas cosas lados de la ecuación.
y5 + 3X2 = Sen X - 4y3
Para el primer y cuarto términos, se utiliza la regla de poder y, debido a que estos términos contienen ys, también utilizan la regla de la cadena. Para el segundo período, se utiliza la regla de la potencia normal. Y para el tercer término, se utiliza la regla sine regular.
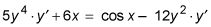
Recoge todos los términos que contienen una
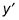
en el lado izquierdo de la ecuación y todos los otros términos en el lado derecho.
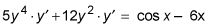
Factorizar
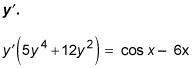
Divida a la respuesta final.
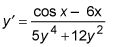
Tenga en cuenta que este derivado se expresa en términos de X y y en lugar de sólo X. Por lo tanto, si desea evaluar la derivada para obtener la pendiente en un punto en particular, es necesario tener valores para ambos X y y para conectar a la derivada.
También tenga en cuenta que en muchos libros de texto, el símbolo
se utiliza en lugar de
en cada paso de soluciones como la que se muestra aquí. Usted puede encontrar
más fácil y menos engorroso para trabajar. Pero
¿Tiene la ventaja de que le recuerda que usted está encontrando la derivada de y con respecto a X. De cualquier manera está bien. Elige tu opción.
-
Comando Derivada de TI-Nspire submenú cálculo cas -
Reglas de cálculo básicas para la economía de la empresa -
Cálculo: cómo resolver los problemas de diferenciación -
Calcular las integrales y representando integrales como funciones -
Distinguir entre las ecuaciones diferenciales lineales, separables y exactas -
Encontrar la integral de un producto de dos funciones
Encuentra la integral de funciones anidadas A veces es necesario integrar una función que es la composición de dos funciones - por ejemplo, la función 2X anidada dentro de una función seno. Si estaba diferenciando, se puede utilizar la regla de la cadena. Desafortunadamente, no existe una…
Cómo coeficientes afectan a la diferenciación Si la función que está diferenciando comienza con un coeficiente, el coeficiente no tiene efecto sobre el proceso de diferenciación. Usted sólo lo ignora y se diferencian de acuerdo a la norma correspondiente. El coeficiente se queda donde…
Cómo determinar los límites de secuencias con l'h & # 244-pital gobierno de Usted puede utilizar la regla de L'H # de 244-pital de encontrar límites de sucesiones. Regla de L'H # de 244-pital es un gran atajo para cuando haces limitar problemas. Aquí está:Convergencia y Divergencia: Usted dice que una secuencia converge…
¿Cómo diferenciar las funciones exponenciales y logarítmicas Diferenciar las funciones exponenciales y logarítmicas implica reglas especiales. No se preocupe - una vez que memorizar un par de reglas, diferenciando estas funciones es un pedazo de pastel.Las funciones exponenciales: Si no puede memorizar esta…
¿Cómo diferenciar funciones inversas Hay una fórmula difícil buscar la participación de las derivadas de las funciones inversas, pero antes de llegar a eso, a ver la figura siguiente, que resume muy bien la idea.Esta cifra muestra un par de funciones inversas, F y g. Funciones…
¿Cómo encontrar derivada de una función mediante el uso de la regla de la cadena La regla de la cadena es de lejos la regla derivada más difícil, pero en realidad no es tan malo si se concentra con cuidado sobre algunos puntos importantes.Por cierto, aquí es una manera de reconocer rápidamente una función compuesta.Cada vez…
¿Cómo encontrar primitivas utilizando reglas inversas Puede utilizar las reglas inversas para encontrar primitivas. Las más sencillas reglas antiderivada son los que son lo contrario de las normas derivadas que ya conoce. Estos son, primitivas automáticos de un solo paso con la excepción de la regla…
¿Cómo encontrar derivados de alto orden Encontrar un segundo, tercero, cuarto, o superior derivado es increíblemente simple. La segunda derivada de una función es simplemente la derivada de su primera derivada. La tercera derivada es la derivada de la segunda derivada, el cuarto…
Cómo utilizar una derivada parcial para medir una pendiente en tres dimensiones Puede utilizar una derivada parcial para medir una tasa de cambio en una dirección de coordenadas en tres dimensiones. Para hacer esto, usted visualiza una función de dos variables z = F(X, y) Como una superficie flotando sobre el xy-plano de un…
Cómo utilizar la diferenciación logarítmica Para diferenciar ciertas funciones, la diferenciación logarítmica es un gran atajo. Se le ahorra el dolor de cabeza de la utilización de la regla del producto o de la multiplicación de todo el asunto y luego diferenciador. Por ejemplo, digamos…
Cómo utilizar la regla de la cadena para encontrar la derivada de funciones anidadas A veces, cuando lo que necesita para encontrar la derivada de una función anidada con la regla de la cadena, averiguar qué función está dentro de lo que puede ser un poco difícil - especialmente cuando una función está anidado dentro de otro…
Las reglas básicas de diferenciación Algunas reglas de diferenciación son muy fácil de recordar y utilizar. Estos incluyen la regla constante, regla de la potencia, la regla múltiplo constante, regla de suma, y la regla diferencia.La regla constante: Este es simple. F (X) = 5…