Cómo utilizar una derivada parcial para medir una pendiente en tres dimensiones
Puede utilizar una derivada parcial para medir una tasa de cambio en una dirección de coordenadas en tres dimensiones. Para hacer esto, usted visualiza una función de dos variables z = F(X, y) Como una superficie flotando sobre el xy-plano de un gráfico cartesiano 3-D. La siguiente figura contiene una función de ejemplo.
Ahora echa un vistazo a la función z = y, se muestra aquí.
Como puede ver, esta función se parece mucho a la cubierta inclinada de una casa. Imagínate a ti mismo de pie en esta superficie. Cuando usted camina en paralelo con el y-eje, la altitud o bien sube o baja. En otras palabras, como el valor de y cambios, también lo hace el valor de z. Pero cuando usted camina en paralelo con el X-eje, la altitud sigue siendo el mismo: el cambio del valor de X no tiene efecto en z.
Así que intuitivamente, se espera que la derivada parcial
es 1. También espera que la derivada parcial
es 0.
Cálculo de derivadas parciales no es mucho más difícil que la evaluación de derivados regulares. Dada una función z(X, y), Las dos derivadas parciales son
He aquí cómo usted calcula ellos:
Calcular
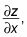
tratar y como una constante y el uso X como la variable de diferenciación.
Calcular
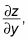
tratar X como una constante y el uso y como la variable de diferenciación.
Por ejemplo, supongamos que usted es dado la ecuación z = 5X2y3. Encontrar
tratar y como si fuera una constante - es decir, tratar todo el factor de 5y3 como si fuera una gran constante - y diferenciar X2:
Encontrar
tratar X como si fuera una constante - es decir, tratar 5X2 como si fuera la constante - y diferenciar y3:
Como otro ejemplo, supongamos que usted es dado la ecuación z = 2eX pecado y + ln X. Encontrar
tratar y como si fuera una constante y diferenciar por la variable X:
Encontrar
tratar X como si fuera una constante y diferenciar por la variable y:
Como se puede ver, al diferenciar por y, los ln X término se trata como una constante y se desvanece por completo.
Volviendo al ejemplo anterior - la " inclinada-techo " función z = y - aquí están las dos derivadas parciales de la función:
Como puede ver, este cálculo produce los resultados previstos.
-
Argumentos Const son un problema constante en c ++ - Cómo utilizar la palabra clave const en C ++
- Constantes PHP
-
Reglas de cálculo básicas para la economía de la empresa -
Cómo utilizar el cálculo con la elección del consumidor en la economía de la empresa -
Modo de empleo derivadas parciales en economía de la empresa
Cómo utilizar la función lagrangiano en economía de la empresa Situaciones de negocios se complican aún más por las limitaciones, que pueden ser contabilizadas en economía de la empresa utilizando el La función de Lagrange. Tal vez la empresa ha firmado un contrato para producir 1.000 unidades del bien al…
Cálculo: cómo resolver los problemas de diferenciación En cálculo, la forma de resolver un problema derivado depende de qué forma el problema toma. Tipos de problemas comunes incluyen la cadena REGLA posición Optimization, la velocidad y las tasas acceleration- y relacionados. Aquí están algunas…
Cálculo II para dummies La siguiente tabla muestra cómo diferenciar e integrar 18 de las funciones más comunes. Como puede ver, la integración invierte diferenciación, devolviendo la función a su estado original, hasta una constante C.La fórmula de Riemann Sum Para…
Cómo coeficientes afectan a la diferenciación Si la función que está diferenciando comienza con un coeficiente, el coeficiente no tiene efecto sobre el proceso de diferenciación. Usted sólo lo ignora y se diferencian de acuerdo a la norma correspondiente. El coeficiente se queda donde…
Cómo descomponer fracciones parciales Un proceso llamado fracciones parciales toma un fracción y la expresa como la suma o diferencia de otras dos fracciones. En cálculo, este proceso es útil antes de integrar una función. Debido a que la integración es mucho más fácil cuando el…
Descomponer fracciones parciales en 8 pasos Cuando su instructor de pre-cálculo le pide que para descomponer fracciones parciales, que en realidad no es tan complicado como parece. El proceso de descomponer una fracción parcial requiere para separar la fracción en dos fracciones (o a veces…
¿Cómo diferenciar funciones inversas Hay una fórmula difícil buscar la participación de las derivadas de las funciones inversas, pero antes de llegar a eso, a ver la figura siguiente, que resume muy bien la idea.Esta cifra muestra un par de funciones inversas, F y g. Funciones…
¿Cómo diferenciar implícitamente A veces se le pide para diferenciar una ecuación que no está resuelto por y, como y5 + 3X2 = Sen X - 4y3. Esta ecuación define y de forma implícita como una función de X, y no se puede escribir como una función explícita porque no puede ser…
¿Cómo encontrar derivada de una función mediante el uso de la regla de la cadena La regla de la cadena es de lejos la regla derivada más difícil, pero en realidad no es tan malo si se concentra con cuidado sobre algunos puntos importantes.Por cierto, aquí es una manera de reconocer rápidamente una función compuesta.Cada vez…
¿Cómo encontrar derivados de alto orden Encontrar un segundo, tercero, cuarto, o superior derivado es increíblemente simple. La segunda derivada de una función es simplemente la derivada de su primera derivada. La tercera derivada es la derivada de la segunda derivada, el cuarto…
¿Cómo integrar composiciones de funciones Las composiciones de funciones - es decir, una función anidada dentro de otra - son de la forma F(g(X)). Usted puede integrarlos sustituyendo u = g(X) cuandoUsted sabe cómo integrar la función externa F.La función interna g(X) diferencia a una…
La identificación, y ecuaciones diferenciales parciales lineales ordinarias Ecuaciones diferenciales (DES) vienen en muchas variedades. Y diferentes variedades de ED se pueden resolver utilizando diferentes métodos. Puede clasificar DES como Des ordinaria y parcial. Además de esta distinción se pueden distinguir…