Modo de empleo derivadas parciales en economía de la empresa

En la mayoría de los casos, dos funciones variables son demasiado simplista para describir una situación adecuada en lo que respecta a la utilización de cálculo en economía de la empresa. Cuando las funciones tienen tres o más variables (dos o más variables independientes), los economistas con frecuencia que desee centrarse en cómo los cambios en el valor de una variable independiente afectan el valor de la variable dependiente.

Considere una situación en la que la cantidad vendida del producto de su empresa depende del precio del producto, p, ingresos de los consumidores, Y, y la cantidad de dinero que se gasta en publicidad, LA, o

Usted puede ser el principal interesado en cómo su publicidad afecta la cantidad vendida.

Para determinar esta relación, se desea determinar el efecto incremental o marginal que la publicidad tiene en la cantidad, q, mientras se mantiene todo lo demás - las demás variables independientes - constante.

Obtener esta información tomando la derivada parcial de la función con respecto a la publicidad.

Usted obtiene un derivada parcial mediante la aplicación de las reglas para la búsqueda de un derivado, mientras que el tratamiento de todas las variables independientes, excepto el de interés, como constantes. Así, en el ejemplo, se mantiene constante tanto en precio y los ingresos. Y la gran cosa acerca de las constantes es su derivada es igual a cero!

Supongamos la siguiente ecuación describe la relación entre la cantidad vendida de un bien y su precio, ingresos de los consumidores, y la cantidad que se gasta en publicidad

dónde q es el número de unidades vendidas por mes, p es el precio por unidad en dólares, Y es el ingreso promedio de los consumidores en dólares, y LA es los gastos de publicidad en dólares.

Con el fin de determinar la derivada parcial de la cantidad con respecto a la publicidad, usted debe tomar los siguientes pasos:

1. En primer lugar, recordar que tanto p y Y se tratan como constantes. Por lo tanto, se les trata exactamente como lo haría un número al tomar la derivada.

2. Para tomar la derivada parcial de q con respecto a LA, comenzar con el primer término " 1000 " y su derivado es igual a cero en la derivada parcial.

3. El segundo término " -10p" tiene una derivada parcial igual a cero porque usted trata a la p como una constante o un número.

4. La próxima legislatura " 0,01Y" también tiene una derivada parcial igual a cero porque usted trata a la Y como una constante.

5. El derivado del término " 0,2LA" es igual a 0.2, porque usted trata a la LA como una variable en esta derivada parcial. Usted está interesado en la determinación de cómo los cambios en LA'valor de s afecta q.

6. El derivado del término " -0,01LAXp" es igual a -0.01p. Recuerde, usted trata p el mismo que cualquier número, mientras LA es la variable.

7. Finalmente, derivado del término " -0.0001LA²" es igual a -0,0002LA.

   Poner cada uno de estos pasos juntos produce una derivada parcial de q con respecto a LA de

   

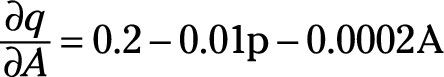
Del mismo modo, la derivada parcial de la cantidad con respecto al precio, # 948-q/ # 948-p, y la derivada parcial de q con respecto a Y, # 948-q/ # 948-Y, se puede determinar mediante el tratamiento de las variables distintas de las especificadas en la derivada parcial como constantes. Esos derivadas parciales serían

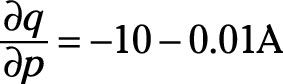
y