Reglas de cálculo básicas para la economía de la empresa

He aquí un breve repaso de algunas de las reglas importantes de la diferenciación de cálculo para la economía de la empresa. Mientras que el cálculo no es necesario, que hace que las cosas más fáciles.

Regla de la función constante

Si la variable y es igual a alguna constante la, su derivada con respecto a X es 0, o si

Por ejemplo,

Regla de la función de energía

Una función de potencia indica que la variable X se eleva a una potencia constante k.

La derivada de y con respecto a X es igual a k multiplicada por X elevado a la k-1 poder, o

Por ejemplo,

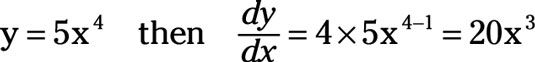
La regla de función de potencia es muy potente! Se puede utilizar con una variedad de exponentes. Por ejemplo,

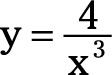
se puede reescribir como

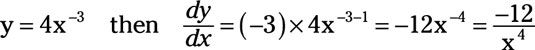
Tenga cuidado con esta última derivada. Cuando una variable con un exponente aparece en el denominador, tales como x³ en la ecuación anterior, la variable puede ser movido al numerador, pero el exponente se convierte en negativo. Por lo tanto, 4 / x³ convierte 4x^-3. Luego, cuando se toma la derivada, asegúrese de que se resta 1 de -3 a conseguir -4.

Como otro ejemplo, considere

puede escribirse como

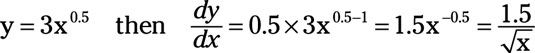
Usted puede recordar que las raíces cuadradas son exponentes fraccionarios o el (la mitad) de potencia 0.5.

Por último, señalar que

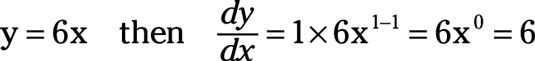
Regla de suma de diferencias

Supongamos que hay dos funciones, TR = g(q) Y TC = h(q).

Usted puede pensar de la variable TR como los ingresos totales, la variable TC como el costo total, y la variable q como la cantidad de producto producido. El símbolo g en la función de los ingresos totales y el símbolo h en la función de costo total significa que la relación entre q y los ingresos totales es diferente de la relación entre q y el costo total.

Además, se supone que la variable # 240- (beneficio) es una función tanto de TR y TC, así

# 240- = TR - TC.

La derivada de # 240- con respecto a q es igual a la suma (las funciones se pueden sumar o restar) de los derivados de TR y TC con respecto a q, o,

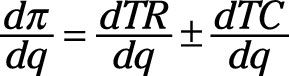
Por ejemplo,

Entonces los derivados de TR y TC con respecto a q son

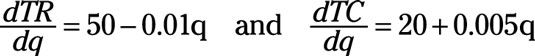
Usando la regla de suma diferencia

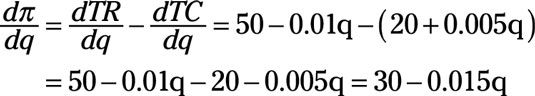
Aunque en el ejemplo se restaron las dos funciones, recuerde que la norma diferencia suma también funciona cuando se añaden funciones.

Estado del producto

Suponga que tiene dos funciones, u = g(X) Y v = h(X). Además, suponer que y = u X v.

La derivada de y con respecto a X es igual a la suma de u multiplicado por la derivada de v y v multiplicado por la derivada de u, o si

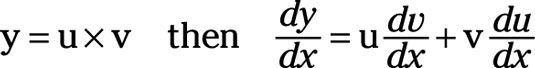
Por ejemplo, si

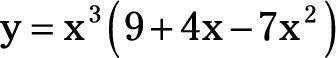
En esta ecuación, u = x³ y v = (9 + 4x - 7x²). Por lo tanto, la derivada de u con respecto a X es

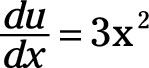
Y el derivado de v con respecto a X es

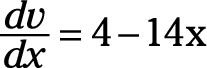
entonces

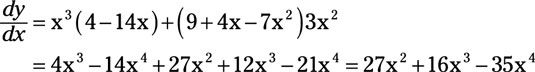
Regla del cociente

Un cociente se refiere al resultado obtenido cuando uno cantidad, en el numerador, se divide por otra cantidad, en el denominador.

Suponga que tiene dos funciones, u = g(X) Y v = h(X). Por lo tanto, u es la cantidad en el numerador, y es una función g de X. Y v es la cantidad en el denominador, y es una función diferente de X como se representa por h. Además, se supone que y = u/v. Así y es el cociente de u Dividido por v.

La derivada de y con respecto a X tiene dos componentes en su numerador. El primer componente es la ecuación original para v multiplicado por la derivada de u adoptar con respecto al X, du / dx. De esa cantidad, se resta segundo componente del numerador, la ecuación original u multiplicado por la derivada de v adoptar con respecto al X, dv / dx.

El dominador de este derivado es simplemente la ecuación original, v, al cuadrado. Por lo tanto,

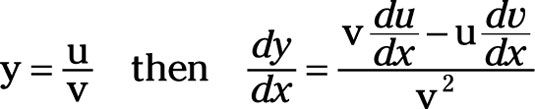
Por ejemplo, si el cociente original es

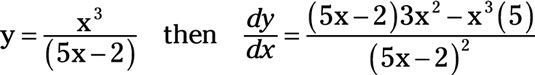
En este cociente, u = X³ y v = (5X - 2). La derivada de u con respeto X es

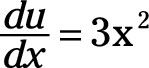
Y el derivado de v con respecto a X es

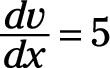
Por lo tanto, el primer componente del numerador es v multiplicado du / dx. A partir de eso, se resta el segundo componente del numerador, que es u multiplicada por dv / dx, o

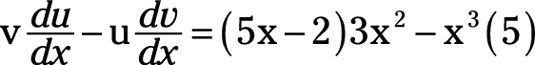
El denominador es v² o

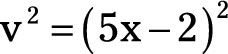
Sustituyendo todo en los rendimientos de la regla del cociente

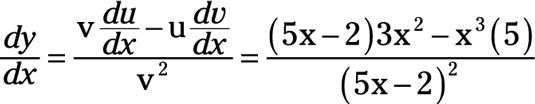
Regla de la cadena

Ya casi ha terminado, y seguro que está pensando, " No es un momento demasiado pronto ". Sólo una regla más se suele utilizar en economía de la empresa - la regla de la cadena.

Para la regla de la cadena, se asume que una variable z es una función de y- eso es, z = F(y). Además, se supone que y es una función de X- eso es, y = g(X). La derivada de z con respecto a X es igual a la derivada de z con respecto a y multiplicado por la derivada de y con respecto a X, o

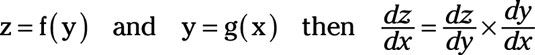
Por ejemplo, si

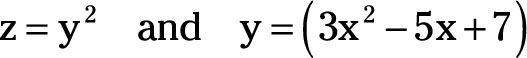
entonces

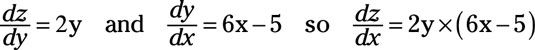
Sustituyendo y = (3X² - 5X +7) en dz / dx rendimientos

Con este último cambio, se quita la tercera variable y a partir del derivado, y como resultado, tiene una función para dz / dx sólo en términos de X.