Saber cuándo integrar por partes
Es importante reconocer que la integración por partes es útil. Para empezar, aquí hay dos casos importantes cuando la integración por partes es definitivamente el camino a seguir:
La función logarítmica ln X
Las cuatro primeras funciones trigonométricas inversas (arcsin X, arccos X, arctan X, y arccot X)
Más allá de estos casos, la integración por partes es útil para integrar el producto de más de un tipo de función o clase de función. Por ejemplo:
X ln X
X segundos de arco X
X2 pecado X
eX cos X
Observe que, en cada caso, se puede reconocer el producto de funciones porque la variable X aparece más de una vez en la función.
Cada vez que te enfrentas a integrar el producto de funciones, considere la sustitución de variables antes de pensar en la integración por partes. Por ejemplo, X cos (X2) Es un trabajo para la sustitución de variables, no integración por partes.
Cuando usted decide utilizar la integración por partes, la siguiente pregunta es cómo dividir la función y asignar las variables u y dv. Afortunadamente, existe una regla mnemotécnica útil para tomar esta decisión: Lovely yontegrals LAre Terrific, que significa Logarithmic, yonverse trig, LAlgebraic, Tequipo de perforación. (Si lo prefiere, también puede utilizar la tecla de acceso Lousy yontegrals LAre Terrible.) Elija siempre el primero función en esta lista como el factor que iguala a u, y luego establecer el resto del producto (incluyendo dx) igual a dv.
Puede utilizar la integración por partes para integrar cualquiera de las funciones enumeradas en la tabla.
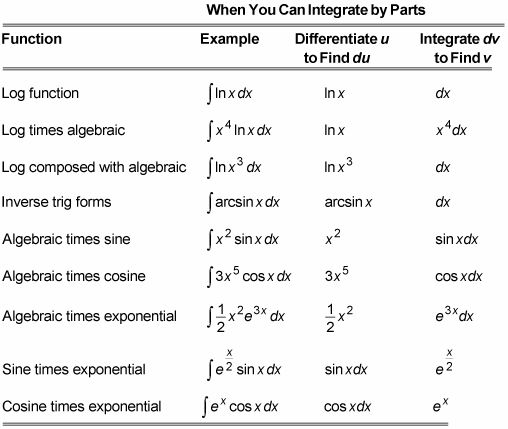
Cuando usted está integrando por partes, aquí está la regla más básica al decidir qué plazo para integrar y que diferenciar: Si sólo conoce la forma de integrar sólo una de las dos, eso es el que más te integras!
-
Cálculo: técnicas de integración -
Cálculo II para dummies -
Calcular las integrales y representando integrales como funciones -
Encontrar la integral de un producto de dos funciones -
Encuentra la integral de funciones anidadas -
Cómo antidifferentiate cualquier polinomio utilizando la suma, constante múltiple, y las reglas de alimentación
¿Cómo se hace la integración por partes Integrando por partes es la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que no puede hacerlo en un producto simple, menos un integrante que…
¿Cómo se hace la integración por partes más de una vez A veces hay que utilizar el método de integración por partes más de una vez porque la primera jugada de ataque por el método que toma sólo parte del camino a la respuesta.Baja por la LIATE lista y escoja u.Utilizando el LIATE recurso…
Cómo hacer una integración sencilla de las piezas Integrando por partes es la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que no puede hacerlo en un producto simple, menos un integrante que…
¿Cómo integrar una función multiplicada por un conjunto de funciones anidadas A veces es necesario integrar el producto de una función (X) Y una composición de funciones (por ejemplo, la función 3X2 + 7 anidada dentro de una función de raíz cuadrada). Si estaba diferenciando, podría utilizar una combinación de la regla…
¿Cómo integrar potencias impares de senos y cosenos Puede integrar alguna función de la forma pecadom X cosn X cuando m es impar, para cualquier valor real de n. Para este procedimiento, tenga en cuenta el pecado identidad trigonométrica útil2 X + cos2 X = 1. Por ejemplo, aquí es cómo…
¿Cómo integrar expresiones racionales utilizando la suma, constante múltiple, y las reglas de alimentación En muchos casos, puede desenredar expresiones racionales peludas e integrarlos utilizando las reglas anti-diferenciación más la regla de la suma, la Regla múltiplo constante, y la Regla de energía.La regla de la suma para la integración le dice…
¿Cómo integrar los problemas de seno / coseno con una potencia extraña, positivo de coseno Mediante la integración de un integrante trig que incluye coseno, y si el poder del coseno es impar y positivo, puede convertir y luego utilizar la sustitución de integrar. Para hacer esta conversión, lo que necesita saber la identidad de…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver integrales mediante la integración por partes Usted puede pensar en la integración por partes como la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que poder't hacerlo en un producto…
Cómo utilizar identidades para integrar las funciones trigonométricas Usted se sorprenderá de lo mucho que avanzar a menudo se puede hacer cuando se integra una función de trigonometría desconocida por primera ajustar usando las identidades Básica Cinco trig:El poder invisible de estas identidades se encuentra en…
Cómo utilizar la integración por partes Al hacer Cálculo, la fórmula de integración por partes te da la opción de romper el producto de dos funciones a sus factores e integrarlo en una forma alterada. Para utilizar la integración por partes en cálculo, siga estos pasos:Descomponer…
La integración de los poderes de cotangentes y cosecantes Puede integrar poderes de cotangentes y cosecantes similares a la forma de hacer las tangentes y secantes. Por ejemplo, aquí es cómo integrar cuna8 X csc6 X:Despegar un csc2 X y colocarlo junto a la dx:Utilice la identidad trigonométrica 1 +…