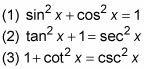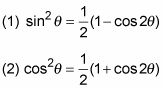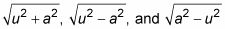Cálculo: técnicas de integración
Usted encontrará que hay muchas maneras de resolver un problema de integración en cálculo. La siguiente lista contiene algunos puntos prácticos para recordar cuando se utilizan diferentes técnicas de integración:
Adivina y Check. Esta técnica funciona cuando el integrando es cerca de un simple derivado hacia atrás.
u-sustitución. La contraparte de integración a la cadena REGLA utilizar esta técnica cuando el argumento de la función que está integrando es más que un simple X.
Integración por partes. Contraparte de Integración a la regla del producto.
1. Utilice esta técnica cuando el integrando contiene un producto de funciones.
2. Escoja su u según LIATE, cuadro que, "7" que, terminarlo.
Trig Integrales
1. Uso identidades pitagóricas.
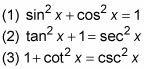
2. Utilice fórmulas medio ángulo.
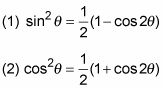
Sustitución trigonométrica. Este método funciona cuando el integrando contiene radicales de las formas
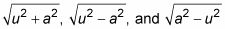
(o poderes de estas raíces), donde la es una constante y u es una expresión en X.
Fracciones parciales. Esta técnica funciona para las funciones racionales (un polinomio sobre otra).
¿Cómo se hace la integración por partes más de una vez A veces hay que utilizar el método de integración por partes más de una vez porque la primera jugada de ataque por el método que toma sólo parte del camino a la respuesta.Baja por la LIATE lista y escoja u.Utilizando el LIATE recurso…
Cómo hacer una integración sencilla de las piezas Integrando por partes es la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que no puede hacerlo en un producto simple, menos un integrante que…
¿Cómo encontrar primitivas con el método de sustitución Cuando el argumento de una función (que es la entrada de la función) es más complicado que algo así como 3X + 2 (a lineal funcion de X - es decir, una función donde X se eleva a la primera potencia), puede utilizar el método de sustitución.…
¿Cómo integrar mediante el uso de fracciones parciales cuando el denominador contiene sólo factores lineales Usted puede utilizar el método de fracciones parciales para integrar funciones racionales (Recordemos que una función racional es uno polinomio dividido por otro.) La idea básica detrás del enfoque de fracciones parciales es " unadding " una…
¿Cómo integrar expresiones racionales utilizando la suma, constante múltiple, y las reglas de alimentación En muchos casos, puede desenredar expresiones racionales peludas e integrarlos utilizando las reglas anti-diferenciación más la regla de la suma, la Regla múltiplo constante, y la Regla de energía.La regla de la suma para la integración le dice…
¿Cómo resolver integrales con la sustitución de variables En cálculo, puede utilizar la sustitución de variables para evaluar una integral compleja. Sustitución de variables permite integrar cuando la regla de la suma, la Regla múltiplo constante, y la Regla de energía no funcionan.Declare una…
¿Cómo resolver integrales mediante la integración por partes Usted puede pensar en la integración por partes como la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que poder't hacerlo en un producto…
Cómo utilizar la integración por partes Al hacer Cálculo, la fórmula de integración por partes te da la opción de romper el producto de dos funciones a sus factores e integrarlo en una forma alterada. Para utilizar la integración por partes en cálculo, siga estos pasos:Descomponer…
Integrar, cuando los poderes de seno, coseno son aún, no negativo Cuando los poderes tanto de seno y coseno son uniformes y no negativo, se puede convertir el integrando en potencias impares de cosenos mediante el uso de las siguientes identidades trigonométricas.Dos identidades trigonométricas prácticos:Luego…
La integración usando fracciones parciales cuando el denominador contiene factores irreducibles cuadráticas Usted puede utilizar el método de fracciones parciales para integrar las funciones racionales, incluyendo funciones con denominadores que contienen irreducible factores de segundo grado (es decir, los factores de segundo grado que no puede…
La integración de los poderes de cotangentes y cosecantes Puede integrar poderes de cotangentes y cosecantes similares a la forma de hacer las tangentes y secantes. Por ejemplo, aquí es cómo integrar cuna8 X csc6 X:Despegar un csc2 X y colocarlo junto a la dx:Utilice la identidad trigonométrica 1 +…
Integración por problemas partes donde usted va en círculos A veces, si se utiliza la integración por partes dos veces, a volver al punto de partida de - que, a diferencia de perderse, no es una pérdida de tiempo.En primer lugar, utilice el LIATE recurso mnemotécnico para recoger su u:Para recoger tu u,…