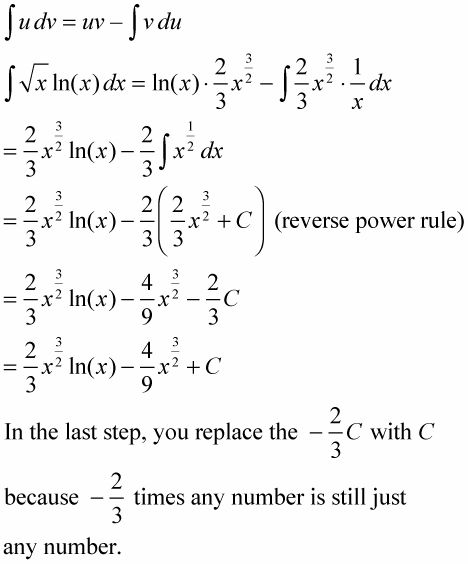Cómo hacer una integración sencilla de las piezas
Integrando por partes es la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que no puede hacerlo en un producto simple, menos un integrante que poder hacer. Aquí está la fórmula:
No trates de entender esto todavía. Espere a los ejemplos que siguen.
Si te acuerdas de eso, usted puede recordar fácilmente que la integral de la derecha es igual que el de la izquierda, excepto con el u y v invertida.
Aquí está el método en una cáscara de nuez.
En primer lugar, tienes que dividir el integrando en un u y un dv para que se ajuste la fórmula. Para este problema, seleccione ln (X) Para que sea su u. Entonces, todo lo demás es la dv, a saber
A continuación, a diferenciar u para obtener su du, y se integra dv para obtener su v. Por último, se conecta todo en la fórmula y ya está en casa gratis.
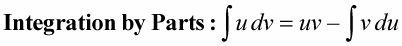
Para ayudar a mantener todo recto, organizar los problemas de integración-by-partes con un cuadro como el que en esta figura. Dibuja una caja vacía de 2 por 2, a continuación, poner su u, ln (X), En la esquina superior izquierda y su dv,
en la esquina inferior derecha, como en la siguiente figura.
Las flechas en esta figura recuerdan a diferenciar a la izquierda y para integrar a la derecha. Piense en la diferenciación - la cosa más fácil - como ir hacia abajo (como ir cuesta abajo), y la integración - la cosa más difícil - como subir (como ir cuesta arriba).
Ahora completar el cuadro:
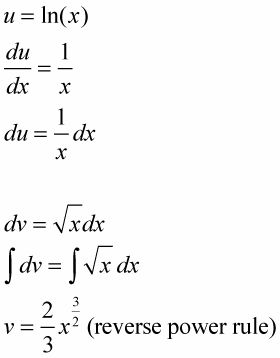
Esta figura muestra el cuadro completo para
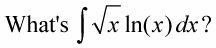
Una buena manera de recordar la fórmula de integración por partes es comenzar en la plaza superior izquierda y sacar un número imaginario 7 - al otro lado, luego hacia abajo a la izquierda, como se muestra en la siguiente figura.
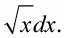
Recordando cómo se dibuja el 7, mira de nuevo a la figura con el cuadro completo. La fórmula de integración por partes te dice que hacer la parte superior de la 7, a saber,
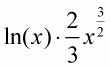
menos la integral de la parte diagonal de la 7,
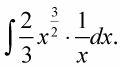
Por cierto, esto es mucho más fácil de hacer que de explicar. Intentalo. Verás cómo este esquema le ayuda a aprender la fórmula y organizar estos problemas.
Listo para terminar? Conecte todo en la fórmula:
Cómo estadísticas muestra la conexión entre la diferenciación y la integración Aún tratando de entender cómo el trabajo de diferenciación e integración? No hay problema: se puede usar las estadísticas para ayudarle. Mediante el estudio de la relación entre dos gráficos simples, vas a entender la relación entre la…
Cómo aproximar área con la regla trapezoidal Con la regla trapezoidal, en lugar de aproximar el área mediante el uso de rectángulos (como lo hace con la izquierda, derecha, y los métodos de rectángulo del punto medio), su área aproximada con - ¿puedes adivinar? - Trapezoides.Debido a la…
Cómo calcular la longitud de arco con la integración Cuando se utiliza la integración para calcular la longitud del arco, lo que está haciendo (tipo de) está dividiendo una longitud de curva en secciones infinitesimalmente pequeñas, calculando la longitud de cada sección pequeña, y luego sumar…
¿Cómo se hace la integración por partes Integrando por partes es la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que no puede hacerlo en un producto simple, menos un integrante que…
¿Cómo se hace la integración por partes más de una vez A veces hay que utilizar el método de integración por partes más de una vez porque la primera jugada de ataque por el método que toma sólo parte del camino a la respuesta.Baja por la LIATE lista y escoja u.Utilizando el LIATE recurso…
Cómo evaluar una integral impropia que es verticalmente infinita Integrales impropias son útiles para resolver una variedad de problemas. LA verticalmente infinita integral impropia contiene al menos una asíntota vertical. Verticalmente integrales impropias infinitos son más difíciles de reconocer que los que…
¿Cómo integrar expresiones racionales utilizando la suma, constante múltiple, y las reglas de alimentación En muchos casos, puede desenredar expresiones racionales peludas e integrarlos utilizando las reglas anti-diferenciación más la regla de la suma, la Regla múltiplo constante, y la Regla de energía.La regla de la suma para la integración le dice…
¿Cómo resolver integrales mediante la integración por partes Usted puede pensar en la integración por partes como la versión de la integración de la regla del producto para la diferenciación. La idea básica de la integración por partes es transformar una integral que poder't hacerlo en un producto…
Cómo utilizar la integración por partes Al hacer Cálculo, la fórmula de integración por partes te da la opción de romper el producto de dos funciones a sus factores e integrarlo en una forma alterada. Para utilizar la integración por partes en cálculo, siga estos pasos:Descomponer…
Integración por problemas partes donde usted va en círculos A veces, si se utiliza la integración por partes dos veces, a volver al punto de partida de - que, a diferencia de perderse, no es una pérdida de tiempo.En primer lugar, utilice el LIATE recurso mnemotécnico para recoger su u:Para recoger tu u,…
Saber cuándo integrar por partes Es importante reconocer que la integración por partes es útil. Para empezar, aquí hay dos casos importantes cuando la integración por partes es definitivamente el camino a seguir:La función logarítmica ln XLas cuatro primeras funciones…
Resolver integrales impropias con uno o dos límites infinitos de integración Cuando integrales impropias tienen uno o dos límites infinitos de integración, puede resolver estas integrales, al convertirlos en los límites donde c tiende a infinito o infinito negativo. He aquí dos ejemplos:Así que esta integral impropia…