Cómo aproximar área con la regla trapezoidal

categoría Educación y lenguas / Matemáticas / Cálculo

Con la regla trapezoidal, en lugar de aproximar el área mediante el uso de rectángulos (como lo hace con la izquierda, derecha, y los métodos de rectángulo del punto medio), su área aproximada con - ¿puedes adivinar? - Trapezoides.

Debido a la forma trapecios abrazan la curva, te dan una mejor estimación de área que cualquiera de los rectángulos izquierdo o derecho. Y resulta que una aproximación trapezoidal es el promedio del rectángulo izquierda y aproximaciones rectángulo de la derecha. ¿Puedes ver por qué? (Sugerencia: El área de cada trapecio es el promedio de las áreas de los dos rectángulos correspondientes en el sumas rectángulo izquierdo y derecho.)

La siguiente figura muestra tres trapecios elaborados bajo la función X2 + 1.

imagen0.jpg

Desde la mirada de esta figura, se podría esperar una aproximación trapezoidal sea mejor que una estimación rectángulo punto medio, pero de hecho, como regla general, sumas punto medio está a punto dos veces mejor que las estimaciones trapezoidales.

Si ya has trabajado a cabo las aproximaciones rectángulo izquierdo y derecho para una función determinada y un cierto número de rectángulos, sólo puede promediar ellos para obtener la estimación trapezoidal correspondiente (por este problema, ya sabes la respuesta que vamos a conseguir es (8 + 17) / 2 = 12,5). Si no es así, aquí está la fórmula:

La regla del trapezoide:

image1.jpg

Para la función en la figura anterior con tres trapecios, aquí está la matemática:

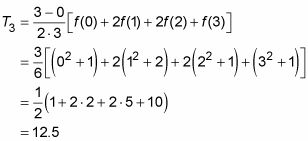
image2.jpg

A pesar de que la definición formal de la integral definida se basa en la suma de un número infinito de rectángulos, es posible que desee pensar en la integración como el límite de la regla trapezoidal en el infinito. Cuanto más te acercas a una curva, la recta se pone. Cuando se utiliza un número cada vez mayor de los trapecios y zoom en donde los trapecios tocan la curva, las copas de los trapecios se acercan cada vez más cerca de la curva. Si te acercas " infinitamente, " la parte superior de la " infinitos " trapezoides se convierten en la curva y, por lo tanto, la suma de sus áreas le da el área bajo la curva exacta. Esta es una buena manera de pensar acerca de por qué la integración produce el área exacta - y tiene sentido conceptual - pero no es en realidad hace de esta manera.



Artículos Relacionados

Sobre el autor
Cómo aproximar el área del punto medio con rectángulos Cómo aproximar el área del punto medio con rectángulos

Una buena manera de aproximarse a las zonas con rectángulos es hacer que cada rectángulo cruzar la curva en el punto medio de la parte superior de ese rectángulo. Una suma punto medio es una mejor estimación del área que cualquiera a la…

Cómo aproximar área con la regla de Simpson Cómo aproximar área con la regla de Simpson

Con la regla de Simpson, que aproximar el área bajo una curva con curvas-coronado " trapezoides ". La parte superior de estas formas son secciones de parábolas. Usted puede llamar " trapezoides " porque juegan el mismo papel en la regla de Simpson…

Cómo calcular la longitud de arco con la integración Cómo calcular la longitud de arco con la integración

Cuando se utiliza la integración para calcular la longitud del arco, lo que está haciendo (tipo de) está dividiendo una longitud de curva en secciones infinitesimalmente pequeñas, calculando la longitud de cada sección pequeña, y luego sumar…

Cómo hacer una aproximación área usando la notación sigma Cómo hacer una aproximación área usando la notación sigma

Notación Sigma es muy útil cuando se está aproximando el área bajo una curva. Por ejemplo, expresar una 8-derecha; aproximación rectángulo del área bajode 0 a 4 y calcular la aproximación.Expresa la idea básica de la suma:Esto sólo…

¿Cómo encontrar el valor medio de una función con el teorema del valor medio para integrales ¿Cómo encontrar el valor medio de una función con el teorema del valor medio para integrales

Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio es con un diagrama - echa un vistazo a continuación.El gráfico…

¿Cómo encontrar el área entre dos curvas ¿Cómo encontrar el área entre dos curvas

Para encontrar el área entre dos curvas, lo que necesita para llegar a una expresión para un rectángulo estrecho que se encuentra en una curva y sube a otro.de X = 0 a X = 1:Para obtener la altura del rectángulo de representación en la figura,…

¿Cómo encontrar el valor medio con el teorema del valor medio para integrales ¿Cómo encontrar el valor medio con el teorema del valor medio para integrales

Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio para integrales es con un diagrama - mira el siguiente figura.El…

Cómo hacer aproximaciones lineales Cómo hacer aproximaciones lineales

Debido a que las funciones ordinarias son localmente lineal (que significa recto) - y cuanto más te acercas a ellos, el más recto que buscar-una línea tangente a una función es una buena aproximación de la función cerca del punto de…

Cómo utilizar la notación sigma para encontrar el área bajo una curva Cómo utilizar la notación sigma para encontrar el área bajo una curva

Puede usar la notación sigma para escribir la suma de Riemann para una curva. Esto es útil cuando se quiere derivar la fórmula para el área aproximada bajo la curva. Por ejemplo, digamos que usted desea encontrar el área aproximada de n…

Cómo escribir sumas de Riemann con la notación sigma Cómo escribir sumas de Riemann con la notación sigma

Puede usar la notación sigma para escribir la derecha; suma rectángulo para una función. Por ejemplo, digamos que tienes F (X) = X2 + 1.Por cierto, no es necesario la notación sigma para la matemáticas que sigue. Es sólo una " conveniencia " -…

La definición de la integral definida y cómo funciona La definición de la integral definida y cómo funciona

Usted puede aproximar el área bajo una curva mediante la suma de la derecha, izquierda o rectángulos punto medio. Para encontrar un área exacta, es necesario utilizar una integral definida.Al aproximar el área bajo una curva, la parte superior…

Cómo calcular el área de un cuadrilátero Cómo calcular el área de un cuadrilátero

Hay cinco fórmulas que se pueden utilizar para calcular el área de las siete cuadriláteros especiales. Sólo hay cinco fórmulas debido a que algunos de ellos lo hacen una doble función - por ejemplo, se puede calcular el área de un rombo con…

» » » » Cómo aproximar área con la regla trapezoidal