¿Cómo encontrar el valor medio con el teorema del valor medio para integrales
Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio para integrales es con un diagrama - mira el siguiente figura.
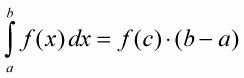
El gráfico de la izquierda muestra un rectángulo cuya área es claramente Menos de el área bajo la curva entre 2 y 5. Este rectángulo tiene una altura igual al punto más bajo en la curva en el intervalo de 2 a 5.
El gráfico central muestra un rectángulo cuya altura es igual al punto más alto de la curva. Su área es claramente mayor de el área bajo la curva. Por ahora usted está pensando, " ¿No hay un rectángulo más alto que la corta y más corta que la altura de un cuya área es lo mismo que el área bajo la curva "? Claro. Y este rectángulo, obviamente, cruza la curva en algún lugar en el intervalo. Este llamado rectángulo valor medio, que se muestra a la derecha, básicamente resume el teorema del valor medio para integrales.
Es sólo sentido común. Pero aquí está la Mumbo Jumbo.
El teorema del valor medio para integrales: Si F (X) Es una función continua en el intervalo cerrado [una B], Entonces existe un número c en el intervalo cerrado de tal manera que
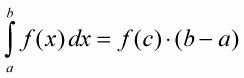
El teorema básicamente sólo garantiza la existencia del rectángulo valor medio.
El área del rectángulo valor medio - que es el mismo como el área bajo la curva - iguales largo veces ancho, o base veces altura, ¿derecho?
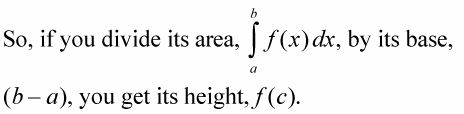
Esta altura es el valor promedio de la función en el intervalo en cuestión.
He aquí un ejemplo. ¿Cuál es la velocidad media de un coche entre t = 9 segundos y t = 16 segundos en cuya velocidad pies per second está dada por la función,
De acuerdo con la definición de valor medio, esta velocidad media está dada por
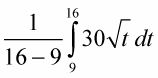
Determinar el área bajo la curva entre 9 y 16.
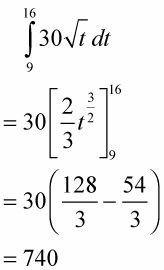
Esta zona, por cierto, es la distancia total recorrida de 9 a 16 segundos. ¿Ve usted por qué? Considere el rectángulo valor medio para este problema. Su altura es de una velocidad (debido a que los valores de la función, o alturas, son las velocidades) y su base es una cantidad de tiempo, por lo que su área es velocidad veces hora que es igual distancia. Por otra parte, recuerda que la derivada de la posición es la velocidad. Así, la primitiva de la velocidad - lo que acabas de hacer en este paso - es la posición, y el cambio de posición de 9 a 16 segundos da la distancia total recorrida.
Dividir esta área, distancia total, por el intervalo de tiempo desde 9 a 16, a saber, 7.
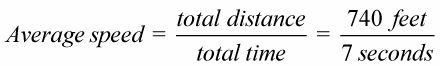
# 8776- 105,7 pies por segundo
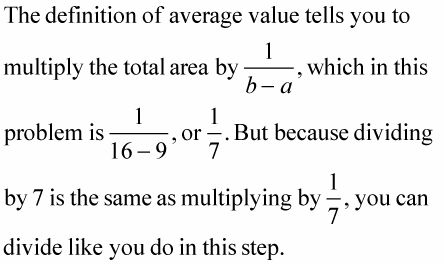
Tiene más sentido pensar en estos problemas en términos de división: zona es igual a base veces altura, por lo que la altura del valor rectángulo media es igual a su área dividido por su base.
Cómo aproximar el área del punto medio con rectángulos Una buena manera de aproximarse a las zonas con rectángulos es hacer que cada rectángulo cruzar la curva en el punto medio de la parte superior de ese rectángulo. Una suma punto medio es una mejor estimación del área que cualquiera a la…
Cómo aproximar área con la regla trapezoidal Con la regla trapezoidal, en lugar de aproximar el área mediante el uso de rectángulos (como lo hace con la izquierda, derecha, y los métodos de rectángulo del punto medio), su área aproximada con - ¿puedes adivinar? - Trapezoides.Debido a la…
Cómo hacer una aproximación área usando la notación sigma Notación Sigma es muy útil cuando se está aproximando el área bajo una curva. Por ejemplo, expresar una 8-derecha; aproximación rectángulo del área bajode 0 a 4 y calcular la aproximación.Expresa la idea básica de la suma:Esto sólo…
¿Cómo encontrar el valor medio de una función con el teorema del valor medio para integrales Usted puede encontrar el valor medio de una función en un intervalo cerrado usando el teorema del valor medio para integrales. La mejor manera de entender el teorema del valor medio es con un diagrama - echa un vistazo a continuación.El gráfico…
¿Cómo encontrar el área con la versión de acceso directo del teorema fundamental del cálculo El teorema fundamental del cálculo tiene una versión de acceso directo que hace que encontrar el área bajo una curva en un instante. Aquí está. Dejar F ser cualquier antiderivada de la función F- despuésCon esta versión del teorema…
¿Cómo encontrar el área entre dos curvas Para encontrar el área entre dos curvas, lo que necesita para llegar a una expresión para un rectángulo estrecho que se encuentra en una curva y sube a otro.de X = 0 a X = 1:Para obtener la altura del rectángulo de representación en la figura,…
¿Cómo medir el cambio de área bajo la curva Puede utilizar una función de área para medir el área bajo una curva, así como la zona cambios. Por ejemplo, digamos que usted tiene cualquier función de edad, F (t). Imagínese que en algún t-valor, lo llaman s, se dibuja una línea vertical…
Cómo utilizar la notación sigma para encontrar el área bajo una curva Puede usar la notación sigma para escribir la suma de Riemann para una curva. Esto es útil cuando se quiere derivar la fórmula para el área aproximada bajo la curva. Por ejemplo, digamos que usted desea encontrar el área aproximada de n…
Calcular rápidamente integrales definidas utilizando el teorema fundamental Este es un teorema de integración atajo requete que utilizará para el resto de tus días naturales nacidos - o por lo menos hasta el final de su temporada con el cálculo. Este método de acceso directo es todo lo que necesita para la mayoría de…
El teorema fundamental del cálculo El teorema fundamental del cálculo es uno de los teoremas más importantes en la historia de las matemáticas. Establece que, dada una función de área LAF que barre área bajo F (t),la velocidad a la que el área está siendo barrido es igual a…
Determinar el área de un triángulo desde su base y la altura Si conoce la base y la altura de un triángulo, puede utilizar una fórmula probada y verdadera para encontrar su área. Es probable que primero encontró con la fórmula básica área del triángulo en aproximadamente sexto o séptimo grado. Si ha…
Cómo calcular el área de un paralelogramo, cometa, o trapezoidal Las fórmulas del área para el paralelogramo, cometa, y trapezoide se basan en el área de un rectángulo. Las siguientes figuras muestran cómo cada uno de estos tres cuadriláteros se refiere a un rectángulo, y la siguiente lista te da los…